Aalto MOOC Matriisilaskenta 2019
Kompleksiluvut
Määritelmä
Kompleksiluku on \(z=x+iy\), missä imaginaariyksikkö \(i\) toteuttaa yhtälön \(i^2=-1\) ja \(x,y\) ovat reaalisia.
- Re\((z)= x\) on \(z\):n reaaliosa.
- Im\((z)= y\) on \(z\):n imaginaariosa.
Esimerkki
Kompleksiluvun \(4-8i\) reaaliosa on \(4\) ja imaginaariosa \(-8\).Perusominaisuuksia
Kompleksiluvut \(z=a+i b\) ja \(w=c+i d\) ovat yhtäsuuret täsmälleen silloin, kun \(a=c\) ja \(b=d\).
Erityisesti kompleksiluku \(z=a+ib\) on nolla täsmälleen silloin, kun \(a=0\) ja \(b=0\).
Vertailuoperaatiot \(<,\leq\) eivät ole määriteltyjä kompleksiluvuille.
Kompleksilukujen laskutoimitukset
Olkoot \(z=a+ib\) ja \(w=c+id\) kompleksilukuja. Tällöin laskutoimitukset saadaan seuraavasti.
Summa:
Erotus:
Tulo:
Osamäärä:
Esimerkki
Olkoon \(z=3+4i\), \(w=1-5i\).
\[z+w=4-i,\] \[z-w=2+9i,\] \[ zw = 3\cdot1+4\cdot5+i(4\cdot 1- 3\cdot 5)=23-11i,\] \[\frac{z}{w} = \Big(\frac{3\cdot 1-4\cdot5}{1^2+5^2}\Big) + i\Big(\frac{4\cdot1+3\cdot5}{1^2+5^2}\Big)= -\frac{17}{26}+\frac{19}{26}i.\]Imaginääriyksikön potenssit
Reaaliluvut ja kompleksiluvut
Jos \(z=a+0i\), niin \(z\) on reaaliluku.
Kaikki tähän mennessä annetut kaavat ovat tosia myös reaaliluvuille.
Jos imaginaariosa on nolla, kaavat palautuvat tunnetuiksi reaalilukujen ominaisuuksiksi.
Kompleksilukujen algebraa
Vaihdannaisuus:
Liitännäisyys
Osittelulaki:
Kompleksikonjugaatti eli liittoluku
Kompleksiluvun \(z=x+iy\) kompleksikonjugaatti eli liittoluku
\(\bar
z\) määritellään
\(\bar z=x-iy\).
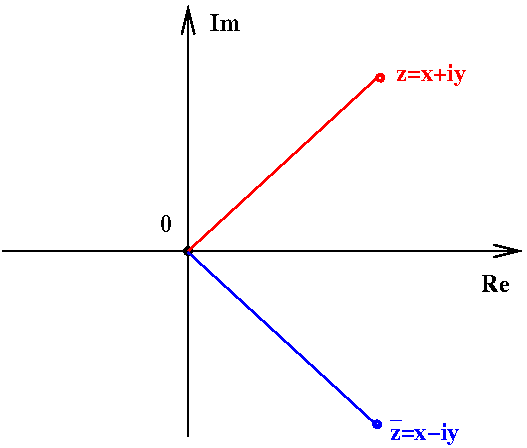
Liittoluvun laskusääntöjä
Seuraus 1: Reaalikertoimiselle kompleksimuuttujan polynomille
pätee \(\overline{P(z)}=P(\bar z)\).
Todistus: Lasketaan
Seuraus 2: Reaalikertoimisen polynomin nollakohta on joko reaalinen tai kompleksisessa tapauksessa liittolukupari.
Todistus:
Olkoon \(z=x+iy\) reaalikertoimisen polynomin \(P\) kompleksinen nollakohta.
Edellisen nojalla saadaan
Kompleksitaso
(Caspar Wessel 1797, Jean Argand 1806)Moduli eli itseisarvo:
Argumentti eli vaihekulma:
Esimerkki
- Olkoon \( z=3+2i\). Laske \[ \text{Re}(1/\bar z^2). \]
- Osoita, että jos \( z\in \mathbb{C}\) ja \( |z|=1\), niin \( \bar z=1/z\).
Ratkaisu:
- Kompleksikonjugaatti: \[ \bar z = 3-2i \] \[ \frac{1}{\bar z^2}=\frac{1}{(3-2i)^2}=\frac{1}{9-12i+4i^2}=\frac{1}{5-12i} \] Lavennetaan nimittäjän kompleksikonjugaatilla: \[ \frac{5+12i}{(5-12i)(5+12i)}=\frac{5+12i}{5^2+12^2}=\frac{5+12i}{169} \] Reaaliosa: \[ \text{Re}\left(\frac{1}{\bar z}\right)=\frac{5}{169}. \]
- Kirjoitetaan, että \( z=x+yi\) \[ |z|=\sqrt{x^2+y^2}=\sqrt{z \bar z} \] \[ |z|=1. \] Saadaan yhtälö \[ \sqrt{z \bar z}=1 \Rightarrow z\bar z=1 \Rightarrow \bar z=\frac{1}{z}. \]
Modulin ominaisuuksia
Koska kompleksiluvun moduli on (positiivinen) reaaliluku, vertailuoperaatiot \(<,\leq,>,\geq\) ovat määriteltyjä.
Kerto ja jakolasku:
Kolmioepäyhtälö:
Argumentin päähaara
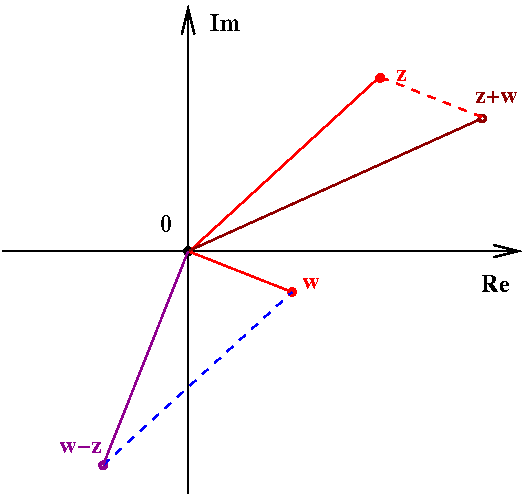
Argumentin arvot ovat välilläYhteen- ja vähennyslaskun geometrinen tulkinta
Kompleksilukujen yhteen- ja vähennyslasku vastaavat vektorien laskutoimituksia.
Polaarimuoto
| Kuvasta nähdään: \[ \left\{ \begin{array}{rcl} x &=&r \cos \theta,\\ y &=& r\sin \theta. \end{array}\right. \] Siis \begin{eqnarray*} z &=& x+iy \\ &=& r\cos \theta +ir \sin \theta. \end{eqnarray*} Saadaan kompleksiluvun esitys polaarimuodossa : \[ z=r(\cos \theta + i \sin\theta). \] | 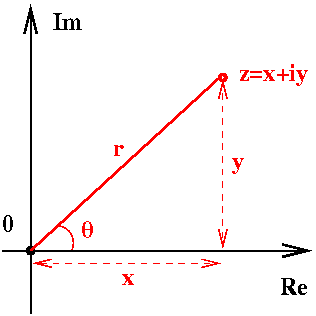 |
Esimerkki
Olkoon \( z_1=1+2i\) ja \( z_2=1-i\) kompleksilukuja.
- Laske \( w=z_1z_2\).
- Laske \( |w|\)
- Esitä luku \( w\) polaarimuodossa.
Ratkaisu:
- \[ w=z_1z_2=(1+2i)(1-i)=1\cdot 1-1\cdot i+2i\cdot 1-2i\cdot i=1+i-2i^2. \] Koska \( i^2=-1\), saadaan \[ w=1+i-2(-1)=3+i. \]
- \[|w|=\sqrt{3^2+1^2}=\sqrt{10}. \]
- Polaarimuoto: \( w=re^{i\varphi}=r(\cos \varphi+i \sin \varphi)\) \[ r=|w|=\sqrt{10} \] \[ \tan \varphi =\frac{y}{x}=\frac{1}{3}\quad \Rightarrow \quad \varphi=\arctan \frac{1}{3} \] \[ w=\sqrt{10} e^{i \arctan \frac{1}{3}}. \]
Eulerin kaava
Eksponenttifunktiolle ja trigonometrisille funktioille ovat voimassa seuraavat sarjaesitykset:
Jos hyväksytään annetut sarjaesitykset, niin:
Seurauksia, identiteetit trigonometrisille funktioille*
Koska
Yleisesti kompleksiluvulle \(z=x+iy\) voidaan kirjoittaa
Kertolaskun geometrinen tulkinta
Sovelletaan Eulerin kaavaa kompleksilukujen kertolaskuun:
Kompleksilukujen kertolaskussa
- Modulit kerrotaan: \(|z_1 z_2| = |z_1||z_2|\).
- Argumentit lasketaan yhteen: \(\arg(z_1z_2)=\arg(z_1)+\arg(z_2)\).
Identiteettejä eksponenttifunktiolle
De Moivren kaava*
Lasketaan esitys kompleksiluvun kokonaislukupotenssille:
Lause (De Moivre)
Kompleksilukujen juuret*
De Moivren kaava on erityisen hyödyllinen etsittäessä kompleksiluvun \(z_0\neq 0\), \(n\):nsiä juuria. Jos \(z^n=z_0\), voidaan kirjoittaa \(z=re^{i\theta}\) ja \(z_0=r_0e^{i\theta_0}\), ja saadaan
Kaikki luvun \(z\) \(n\):net juuret saadaan siis kaavasta
missä \(k\) on mikä tahansa kokonaisluku. Havaitaan myös, että jokainen \(k=0,1,\ldots,n-1\) antaa eri arvon, mutta muut \(k\):n arvot vain toistavat jonkun edellisistä, koska \(e^{2\pi ik}=1\). Siten kompleksiluvulla \(z_0\neq 0\) on täsmälleen \(n\) erillistä \(n\):ttä juurta.
Kaavasta havaitaan myös, että kaikki juurilla on sama itseisarvo \(\sqrt[n]{|z_0|}\), ja argumentit ovat tasavälisiä. Siksi kaikki juuret sijaitsevat origokeskisen ympyrän, jonka säde on \(\sqrt[n]{|z_0|}\) kehällä.
Olemme osoittaneet:
Lause
Jos \(z=re^{i\theta}\neq 0\), yhtälöllä \(w^n=z\) on täsmälleen \(n\) erillistä ratkaisua, jotka saadaan kaavasta
Esimerkki
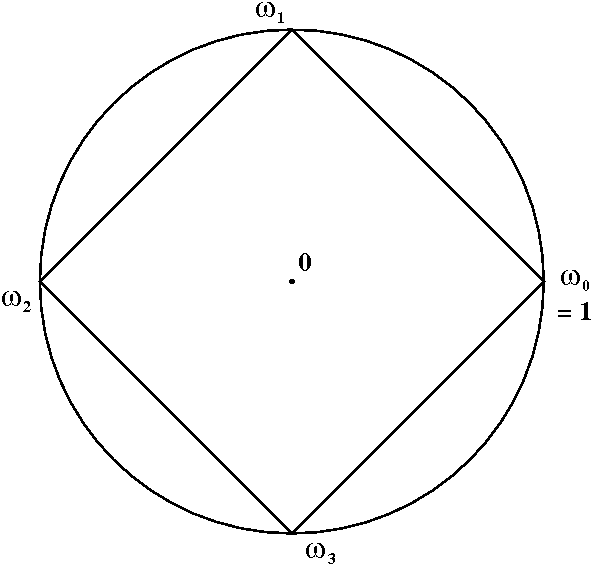
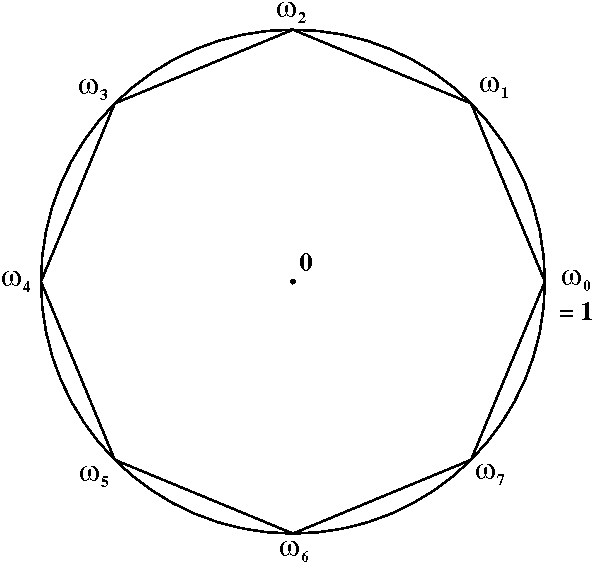
Ykkösen \(n\):net juuret saadaan kaavasta \[ \omega_k = e^{i2k\pi/n}, \qquad k=0,1,\ldots,n-1. \]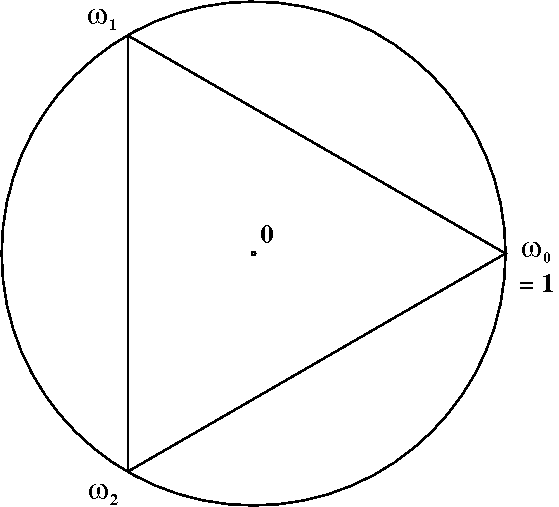
|
|
|
Jos asetetaan \(\omega = e^{2\pi i/n}\), niin kaikki ykkösen \(n\):nnet juuret ovat \(1,\omega,\omega^2,\omega^3,\ldots,\omega^{n-1}\).
Jos \(\omega \neq 1\), saadaan \(\omega^n=1\), eli
\[0=\omega^n-1=(\omega-1)(1+\omega+\omega^2+\ldots+\omega^{n-1}).\]Saadaan:
\[ 1+\omega+\omega^2+\ldots+\omega^{n-1}=0\qquad(\omega=e^{i2\pi/n}). \]Kompleksiset matriisit*
Matriisilaskennassa avaruuden \(\mathbb{C}^n\) alkioita käsitellään sarakevektoreina (pystyvektoreina)
Edellisessä käytettiin aikaisemmin käsiteltyä matriisituloa.
Käytännössä siis lineaarikuvaukset \(\mathbf{A}\colon \mathbb{C}^n \to \mathbb{C}^m\) ja matriisit \(\mathbf{A}\in \mathbb{C}^ {m\times n}\) voidaan samastaa keskenään.
Tällöin kuvausten \( \mathbf{A} \colon \mathbb{C}^n \to \mathbb{C}^p\) ja \(\mathbf{B}\colon \mathbb{C}^p \to \mathbb{C}^m\) yhdistetty kuvaus \(\mathbf{B} \circ \mathbf{A} \colon \mathbb{C}^n \to \mathbb{C}^m\) vastaa matriisituloa \(\mathbf{BA}\in \mathbb{C}^{m\times n}\).
Matriisiyhtälö \(\mathbf{Av}= \mathbf{w}\) vastaa lineaarista yhtälöryhmää
