Piste- eli sisätulo

Tason vektorien \(\mathbf{v}=\begin{pmatrix} v_1 \\ v_2 \end{pmatrix}\) ja \(\mathbf{w}=\begin{pmatrix} w_1 \\ w_2 \end{pmatrix}\) sisätulo \(\mathbf{v\cdot w}\) on luku (skalaari) \(v_1 w_1+ v_2 w_2.\)

Vastaavasti ulottuvuudessa \(n\) sisätulo on määritelty seuraavasti:

\[ \mathbf{v}\cdot \mathbf{w}=\sum\limits_{j=1}^n v_jw_j \] eli summattavien termien määrä vain kasvaa vastaamaan \(n\):ää.

Esimerkki

\[ \mathbf{v}=\begin{pmatrix} 1 \\ 3 \end{pmatrix}, \mathbf{w}=\begin{pmatrix} 2 \\ 4 \end{pmatrix}; \quad \mathbf{v\cdot w}=1\cdot 2+3\cdot 4=14. \]

Huom. Sisätulolle on myös vaihtoehtoinen (yleisempi) merkintätapa: \(\langle\mathbf{v},\mathbf{w}\rangle\).

Vektorin pituus eli normi

Vektorin \(\mathbf{v}\) pituus \(\| \mathbf{v} \|\) määritellään sisätulon avulla:

\[ \| \mathbf{v} \|=\sqrt{\mathbf{v}\cdot \mathbf{v}}. \]

Yksikkövektorin \(\mathbf{u}\) pituus on yksi, tällöin \(\mathbf{u}\cdot \mathbf{u}=1\). Vektorin \(\mathbf{v}\) suuntainen yksikkövektori on \(\frac{\mathbf{v}}{\| \mathbf{v} \|}\).

Esimerkki

\[ \mathbf{v}=\begin{pmatrix} 1 \\ 3 \end{pmatrix}; \quad \|\mathbf{v}\|=\sqrt{\mathbf{v\cdot v}}=\sqrt{1\cdot 1+3\cdot 3}=\sqrt{10}, \] \[ \frac{\mathbf{v}}{\|\mathbf{v}\|}=\frac{1}{\sqrt{10}}\begin{pmatrix} 1 \\ 3 \end{pmatrix}. \]

Yksikköympyrä tasossa

Yksikkövektorit voidaan myös ajatella yksikköympyrän pisteinä ja trigonometrian avulla määritellä kyseisen vektorin ja x-akselin välisen kulman avulla seuraavasti:
\[ \mathbf{u\cdot i} = \cos \theta \] \[ \mathbf{u\cdot j} = \sin \theta \] 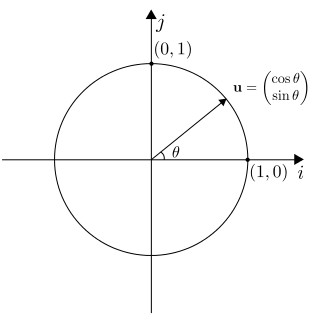Yksikköympyrä tasossa

Liikuta yksikköympyrällä olevaa punaista pistettä. Millainen yhteys on pisteen koordinaateilla ja kulman trigonometristen funktioiden arvoilla? Miksi näin on?

Vektoreiden välinen kulma

Vektoreiden kohtisuoruus: Kaksi vektoria \(\mathbf{v}\) ja \(\mathbf{w}\) ovat keskenään kohtisuorassa, jos niiden sisätulo on nolla, eli \(\mathbf{v}\cdot \mathbf{w}=0\).

Kosinikaava

\[ \frac{\mathbf{v}\cdot \mathbf{w}}{\| \mathbf{v}\| \|\mathbf{w}\| }=\cos \theta \]

Kosinikaavan avulla saadaan kaksi epäyhtälöä:

  1. Schwarzin epäyhtälö: \(| \mathbf{v}\cdot \mathbf{w}| \leq \|\mathbf{v}\| \|\mathbf{w} \| \)
  2. Kolmioepäyhtälö: \(\|\mathbf{v}+ \mathbf{w}\| \leq \|\mathbf{v}\| +\|\mathbf{w} \|\)

Kolmioepäyhtälön todistus

\begin{align*} (\mathbf{v}+\mathbf{w})\cdot (\mathbf{v}+\mathbf{w}) & = \mathbf{v}\cdot \mathbf{v}+ \mathbf{v}\cdot \mathbf{w}+ \mathbf{w}\cdot \mathbf{v}+ \mathbf{w}\cdot \mathbf{w} \\ & = \mathbf{v} \cdot \mathbf{v}+ 2\mathbf{v}\cdot \mathbf{w}+ \mathbf{w}\cdot \mathbf{w} \\ & = \| \mathbf{v} \|^2+2\mathbf{v}\cdot \mathbf{w}+ \| \mathbf{w} \|^2 \\ & \leq \| \mathbf{v} \|^2+2\|\mathbf{v} \| \|\mathbf{w} \|+ \|\mathbf{w} \|^2 \\ & = (\|\mathbf{v} \|+\| \mathbf{w} \|)^2. \end{align*}

Esimerkki

Jos \(\mathbf{v}\) ja \(\mathbf{w}\) ovat vektoreita, joille \(\|\mathbf{v}\| = 5\) ja \(\|\mathbf{w}\| = 3\), niin laske

  1. \(\|\mathbf{v} -\mathbf{w} \|\) suurin ja pienin arvo,
  2. \(\mathbf{v} \cdot \mathbf{w}\) suurin ja pienin arvo.

Ratkaisu

Tarvittaessa arvioita vektorien normeille, ehdottomasti tehokkaimmat työkalut ovat kolmioepäyhtälö: \(\big| \|\mathbf{x}\|-\|\mathbf{y}\| \big|\leq \|\mathbf{x}-\mathbf{y}\|\leq \|\mathbf{x}\|+\|\mathbf{y}\|\), sekä Cauchy-Schwarzin epäyhtälö: \(|\mathbf{x}\cdot \mathbf{y}|\leq \|\mathbf{x}\|\|\mathbf{y}\|\).

  1. Aloitetaan arvioimalla lauseketta \(\|\mathbf{v}-\mathbf{w}\|\): \[ \big| \|\mathbf{v}\|-\|\mathbf{w}\| \big|\leq \|\mathbf{v} - \mathbf{w} \| = \|\mathbf{v} + (-\mathbf{w}) \| \leq \|\mathbf{v} \| + \|-\mathbf{w}\| = \|\mathbf{v} \| + \|\mathbf{w}\|. \]

    2. Koska \(\|\mathbf{v}\| = 5 \) ja \(\|\mathbf{w}\| = 3\), saadaan nämä sijoittamalla ala- ja yläraja erotukselle:

    \begin{align*} &\big| 5-3 \big|\leq \|\mathbf{v} - \mathbf{w} \| \leq 5 + 3 \\ &\Rightarrow 2 \leq \| \mathbf{v}-\mathbf{w}\| \leq 8. \end{align*}
  2. Arvioidaan sisätuloa \(\mathbf{v}\cdot \mathbf{w}\). Euklidisessa avaruudessa, kuten \(\mathbb{R}^n\), pistetulon määritelmä on \[ \mathbf{v}\cdot \mathbf{w} = \|\mathbf{v}\| \|\mathbf{w}\| \cos \theta, \] missä \(\theta\) on vektorien väliin jäävä kulma. Koska \(-1\leq \cos \theta \leq 1\), saadaan \begin{align*} -\|\mathbf{v}\| \|\mathbf{w}\| &\leq \mathbf{v}\cdot \mathbf{w} \leq \|\mathbf{v}\| \|\mathbf{w}\| \\ -(5\cdot 3) & \leq \mathbf{v}\cdot \mathbf{w} \leq 5\cdot 3 \\ -15 & \leq \mathbf{v}\cdot \mathbf{w} \leq 15. \end{align*}

Esimerkki

Valitse mitkä tahansa kolme numeroa \(x,y,z\) siten, että \(x+y+z=0\). Mikä on vektorien \(\mathbf{v} = (x,y,z)\) ja \(\mathbf{w} = (z,x,y)\) välinen kulma? Näytä yleisesti, että näin valituilla \(\mathbf{v} , \mathbf{w}\) pätee

\[ \frac{\mathbf{v} \cdot \mathbf{w} }{\|\mathbf{v} \| \|\mathbf{w} \|} = -\frac{1}{2}. \]

Ratkaisu

Yhtälö \(x+y+z=0\) määritteleee origon kautta kulkevan tason \(\mathbb{R}^3\):ssa. Vektorit \(\mathbf{v} = \begin{pmatrix} x \\ y \\ z \end{pmatrix}\) ja \(\mathbf{w} = \begin{pmatrix} z \\ x \\ y \end{pmatrix}\) määrittelevät tämän tason kaksi vektoria, vielä niin, että toisen saa toisesta sopivalla kierrolla.

  1. Aluksi valitaan kolme lukua \(x,y,z\), jotka toteuttavat yhtälön \(x+y+z=0\). Valitaan \(x = 1, y=1,z=-2\), ja lasketaan vektorien \(\mathbf{v}\) ja \(\mathbf{w}\) välinen kulma \(\theta\). Kulman kosini saadaan lauseesta \(\cos \theta = \displaystyle \frac{\mathbf{v}\cdot \mathbf{w}}{\Vert \mathbf{v} \Vert\Vert \mathbf{w} \Vert}\): \( \displaystyle \cos \theta = \frac{-2+1-2}{\sqrt{6}\sqrt{6}} = -\frac{1}{2}\) ja \(\displaystyle \arccos \left( -\frac{1}{2} \right) = \frac{2\pi}{3}\).
  2. Muutaman kokeilun jälkeen vaikuttaisi siltä että riippumatta valituista luvuista \(x,y,z\) vektorien \(\mathbf{v}\) ja \(\mathbf{w}\) välinen kulma on aina sama. Voisiko tämän johtaa yleiseksi säännöksi?

    Aloitetaan kirjoittamlla lauseke \(\displaystyle \frac{\mathbf{v}\cdot \mathbf{w}}{\Vert \mathbf{v} \Vert\Vert \mathbf{w} \Vert}\) auki:

    \[ \frac{\mathbf{v}\cdot \mathbf{w}}{\Vert \mathbf{v} \Vert\Vert \mathbf{w} \Vert} = \frac{xz+yx+zy}{\sqrt{x^2+y^2+z^2}\sqrt{z^2+x^2+y^2}} = \frac{xz+yx+zy}{x^2+y^2+z^2} . \]

    Tämän jälkeen palataan tason yhtälöön \(x+y+z=0\) ja ratkaistaan \(z = -(x+y)\) ja sijoitetaan edelliseen:

    \[ \frac{x(-x-y)+yx+y(-x-y)}{x^2+y^2+(-x-y)^2} = \frac{-x^2-xy-y^2}{2x^2+2xy+2y^2} = -\frac{1}{2}. \]


Pistetulo voidaan siis määritellä vektorien pituuksien ja niiden välisen kulman kosinin arvon tulona. Tutki miten pistetulon arvo muuttuu, kun vektorit liikkuvat tasossa. Tartu punaisen ja sinisen vektorin kärkeen ja siirrä niitä.

Tutki edelleen, missä tilanteessa pistetulon arvo on sama kuin vektorien projektio toisilleen, eli \(\mathbf{a}\cdot\mathbf{b}=\|\mathbf{OC}\|\). Kuvassa vektorin \(\mathbf{b}\) projektio vektorille \(\mathbf{a}\) on kuvattu vihreällä janalla OC.

Yhtälöpari

Tarkastellaan lineaarista yhtälöparia

\[ \left\{ \begin{array}{ll} 4x_1-2x_2 & = 2 \\ x_1+x_2 & = 5 \end{array} \right. \]

Ratkaistaan yhtälöpari käyttämällä yhteenlaskumenetelmää. Kerrotaan alempi yhtälö 2:lla ja lasketaan yhtälöt yhteen, jolloin \(x_2\):t kumoutuvat ja saadaan yhtälö, jossa on vain yhtä muuttujaa. Operaatio säilyttää yhtäsuuruuden, sillä alemman yhtälön molemmille puolille summataan yhtäsuuret lausekkeet:

\[ \left\{ \begin{array}{ll} 4x_1-2x_2 & = 2 \\ 2x_1+2x_2 & = 10 \end{array} \right. \]
\[ \begin{array}{rl} 2x_1+2x_2+(4x_1-2x_2) &= 10 + 2 \\ 6x_1 &=12 \\ x_1& =2 \end{array} \]

Sijoittamalla tämä \(x_1\):n arvo alempaan yhtälöön saadaan \( 2+x_2=5 \Rightarrow x_2=3\). Yhtälöparin ratkaisu on siis

\[ \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}= \begin{pmatrix} 2 \\ 3 \end{pmatrix}. \]

Huomaa, että kumpikin esimerkin yhtälö kuvaa suoraa tasossa \( \mathbb{R}^2 \), ja yhtälöparin ratkaisu \( (x_1,x_2)\) on suorien leikkauspiste. Yleisemmin, yhtälöparilla voi olla joko 0 (kaksi samansuuntaista suoraa), 1 (kaksi leikkaavaa suoraa) tai äärettömän monta (päällekkäiset suorat) ratkaisua.

Остання зміна: четвер 5 жовтня 2017 13:09 PM