Aalto MOOC Matriisilaskenta 2019
Vektorien sisätulo, pituus ja yhtälöryhmät
Piste- eli sisätulo
Tason vektorien \(\mathbf{v}=\begin{pmatrix} v_1 \\ v_2 \end{pmatrix}\) ja \(\mathbf{w}=\begin{pmatrix} w_1 \\ w_2 \end{pmatrix}\) sisätulo \(\mathbf{v\cdot w}\) on luku (skalaari) \(v_1 w_1+ v_2 w_2.\)
Vastaavasti ulottuvuudessa \(n\) sisätulo on määritelty seuraavasti:
Esimerkki
\[ \mathbf{v}=\begin{pmatrix} 1 \\ 3 \end{pmatrix}, \mathbf{w}=\begin{pmatrix} 2 \\ 4 \end{pmatrix}; \quad \mathbf{v\cdot w}=1\cdot 2+3\cdot 4=14. \]Huom. Sisätulolle on myös vaihtoehtoinen (yleisempi) merkintätapa: \(\langle\mathbf{v},\mathbf{w}\rangle\).
Vektorin pituus eli normi
Vektorin \(\mathbf{v}\) pituus \(\| \mathbf{v} \|\) määritellään sisätulon avulla:
Yksikkövektorin \(\mathbf{u}\) pituus on yksi, tällöin \(\mathbf{u}\cdot \mathbf{u}=1\). Vektorin \(\mathbf{v}\) suuntainen yksikkövektori on \(\frac{\mathbf{v}}{\| \mathbf{v} \|}\).
Esimerkki
\[ \mathbf{v}=\begin{pmatrix} 1 \\ 3 \end{pmatrix}; \quad \|\mathbf{v}\|=\sqrt{\mathbf{v\cdot v}}=\sqrt{1\cdot 1+3\cdot 3}=\sqrt{10}, \] \[ \frac{\mathbf{v}}{\|\mathbf{v}\|}=\frac{1}{\sqrt{10}}\begin{pmatrix} 1 \\ 3 \end{pmatrix}. \]
Yksikköympyrä tasossa
Yksikkövektorit voidaan myös ajatella yksikköympyrän pisteinä ja trigonometrian avulla määritellä kyseisen vektorin ja x-akselin välisen kulman avulla seuraavasti:| \[ \mathbf{u\cdot i} = \cos \theta \] \[ \mathbf{u\cdot j} = \sin \theta \] | 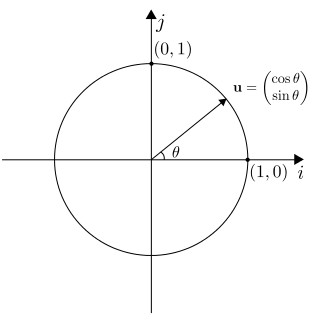
|
Liikuta yksikköympyrällä olevaa punaista pistettä. Millainen yhteys on pisteen koordinaateilla ja kulman trigonometristen funktioiden arvoilla? Miksi näin on?
Vektoreiden välinen kulma
Vektoreiden kohtisuoruus: Kaksi vektoria \(\mathbf{v}\) ja \(\mathbf{w}\) ovat keskenään kohtisuorassa, jos niiden sisätulo on nolla, eli \(\mathbf{v}\cdot \mathbf{w}=0\).
Kosinikaava
Kosinikaavan avulla saadaan kaksi epäyhtälöä:
- Schwarzin epäyhtälö: \(| \mathbf{v}\cdot \mathbf{w}| \leq \|\mathbf{v}\| \|\mathbf{w} \| \)
- Kolmioepäyhtälö: \(\|\mathbf{v}+ \mathbf{w}\| \leq \|\mathbf{v}\| +\|\mathbf{w} \|\)
Kolmioepäyhtälön todistus
Esimerkki
Jos \(\mathbf{v}\) ja \(\mathbf{w}\) ovat vektoreita, joille \(\|\mathbf{v}\| = 5\) ja \(\|\mathbf{w}\| = 3\), niin laske
- \(\|\mathbf{v} -\mathbf{w} \|\) suurin ja pienin arvo,
- \(\mathbf{v} \cdot \mathbf{w}\) suurin ja pienin arvo.
Ratkaisu
Tarvittaessa arvioita vektorien normeille, ehdottomasti tehokkaimmat työkalut ovat kolmioepäyhtälö: \(\big| \|\mathbf{x}\|-\|\mathbf{y}\| \big|\leq \|\mathbf{x}-\mathbf{y}\|\leq \|\mathbf{x}\|+\|\mathbf{y}\|\), sekä Cauchy-Schwarzin epäyhtälö: \(|\mathbf{x}\cdot \mathbf{y}|\leq \|\mathbf{x}\|\|\mathbf{y}\|\).
- Aloitetaan arvioimalla lauseketta \(\|\mathbf{v}-\mathbf{w}\|\): \[ \big| \|\mathbf{v}\|-\|\mathbf{w}\| \big|\leq \|\mathbf{v} - \mathbf{w} \| = \|\mathbf{v} + (-\mathbf{w}) \| \leq \|\mathbf{v} \| + \|-\mathbf{w}\| = \|\mathbf{v} \| + \|\mathbf{w}\|. \]
- Arvioidaan sisätuloa \(\mathbf{v}\cdot \mathbf{w}\). Euklidisessa avaruudessa, kuten \(\mathbb{R}^n\), pistetulon määritelmä on \[ \mathbf{v}\cdot \mathbf{w} = \|\mathbf{v}\| \|\mathbf{w}\| \cos \theta, \] missä \(\theta\) on vektorien väliin jäävä kulma. Koska \(-1\leq \cos \theta \leq 1\), saadaan \begin{align*} -\|\mathbf{v}\| \|\mathbf{w}\| &\leq \mathbf{v}\cdot \mathbf{w} \leq \|\mathbf{v}\| \|\mathbf{w}\| \\ -(5\cdot 3) & \leq \mathbf{v}\cdot \mathbf{w} \leq 5\cdot 3 \\ -15 & \leq \mathbf{v}\cdot \mathbf{w} \leq 15. \end{align*}
Koska \(\|\mathbf{v}\| = 5 \) ja \(\|\mathbf{w}\| = 3\), saadaan nämä sijoittamalla ala- ja yläraja erotukselle:
\begin{align*} &\big| 5-3 \big|\leq \|\mathbf{v} - \mathbf{w} \| \leq 5 + 3 \\ &\Rightarrow 2 \leq \| \mathbf{v}-\mathbf{w}\| \leq 8. \end{align*}
Esimerkki
Valitse mitkä tahansa kolme numeroa \(x,y,z\) siten, että \(x+y+z=0\). Mikä on vektorien \(\mathbf{v} = (x,y,z)\) ja \(\mathbf{w} = (z,x,y)\) välinen kulma? Näytä yleisesti, että näin valituilla \(\mathbf{v} , \mathbf{w}\) pätee
\[ \frac{\mathbf{v} \cdot \mathbf{w} }{\|\mathbf{v} \| \|\mathbf{w} \|} = -\frac{1}{2}. \]Ratkaisu
Yhtälö \(x+y+z=0\) määritteleee origon kautta kulkevan tason \(\mathbb{R}^3\):ssa. Vektorit \(\mathbf{v} = \begin{pmatrix} x \\ y \\ z \end{pmatrix}\) ja \(\mathbf{w} = \begin{pmatrix} z \\ x \\ y \end{pmatrix}\) määrittelevät tämän tason kaksi vektoria, vielä niin, että toisen saa toisesta sopivalla kierrolla.
- Aluksi valitaan kolme lukua \(x,y,z\), jotka toteuttavat yhtälön \(x+y+z=0\). Valitaan \(x = 1, y=1,z=-2\), ja lasketaan vektorien \(\mathbf{v}\) ja \(\mathbf{w}\) välinen kulma \(\theta\). Kulman kosini saadaan lauseesta \(\cos \theta = \displaystyle \frac{\mathbf{v}\cdot \mathbf{w}}{\Vert \mathbf{v} \Vert\Vert \mathbf{w} \Vert}\): \( \displaystyle \cos \theta = \frac{-2+1-2}{\sqrt{6}\sqrt{6}} = -\frac{1}{2}\) ja \(\displaystyle \arccos \left( -\frac{1}{2} \right) = \frac{2\pi}{3}\).
- Muutaman kokeilun jälkeen vaikuttaisi siltä että riippumatta valituista luvuista \(x,y,z\) vektorien \(\mathbf{v}\) ja \(\mathbf{w}\) välinen kulma on aina sama. Voisiko tämän johtaa yleiseksi säännöksi?
Aloitetaan kirjoittamlla lauseke \(\displaystyle \frac{\mathbf{v}\cdot \mathbf{w}}{\Vert \mathbf{v} \Vert\Vert \mathbf{w} \Vert}\) auki:
\[ \frac{\mathbf{v}\cdot \mathbf{w}}{\Vert \mathbf{v} \Vert\Vert \mathbf{w} \Vert} = \frac{xz+yx+zy}{\sqrt{x^2+y^2+z^2}\sqrt{z^2+x^2+y^2}} = \frac{xz+yx+zy}{x^2+y^2+z^2} . \]Tämän jälkeen palataan tason yhtälöön \(x+y+z=0\) ja ratkaistaan \(z = -(x+y)\) ja sijoitetaan edelliseen:
\[ \frac{x(-x-y)+yx+y(-x-y)}{x^2+y^2+(-x-y)^2} = \frac{-x^2-xy-y^2}{2x^2+2xy+2y^2} = -\frac{1}{2}. \]
Pistetulo voidaan siis määritellä vektorien pituuksien ja niiden välisen kulman kosinin arvon tulona. Tutki miten pistetulon arvo muuttuu, kun vektorit liikkuvat tasossa. Tartu punaisen ja sinisen vektorin kärkeen ja siirrä niitä.
Tutki edelleen, missä tilanteessa pistetulon arvo on sama kuin vektorien projektio toisilleen, eli \(\mathbf{a}\cdot\mathbf{b}=\|\mathbf{OC}\|\). Kuvassa vektorin \(\mathbf{b}\) projektio vektorille \(\mathbf{a}\) on kuvattu vihreällä janalla OC.
Yhtälöpari
Tarkastellaan lineaarista yhtälöparia
Ratkaistaan yhtälöpari käyttämällä yhteenlaskumenetelmää. Kerrotaan alempi yhtälö 2:lla ja lasketaan yhtälöt yhteen, jolloin \(x_2\):t kumoutuvat ja saadaan yhtälö, jossa on vain yhtä muuttujaa. Operaatio säilyttää yhtäsuuruuden, sillä alemman yhtälön molemmille puolille summataan yhtäsuuret lausekkeet:
Sijoittamalla tämä \(x_1\):n arvo alempaan yhtälöön saadaan \( 2+x_2=5 \Rightarrow x_2=3\). Yhtälöparin ratkaisu on siis
Huomaa, että kumpikin esimerkin yhtälö kuvaa suoraa tasossa \( \mathbb{R}^2 \), ja yhtälöparin ratkaisu \( (x_1,x_2)\) on suorien leikkauspiste. Yleisemmin, yhtälöparilla voi olla joko 0 (kaksi samansuuntaista suoraa), 1 (kaksi leikkaavaa suoraa) tai äärettömän monta (päällekkäiset suorat) ratkaisua.
