Differentiaali- ja integraalilaskenta 2, kevät 2022 (Aalto MOOC)

Napakoordinaatit

Piste \((x,y)\in \mathbb{R}^2\) voidaan kirjoittaa muodossa \((r,\theta)\), missä \(r\geq0\) ja \(0\le \theta < 2\pi\). Napakulma \(\theta\) on yksikäsitteinen jos \(r > 0\).

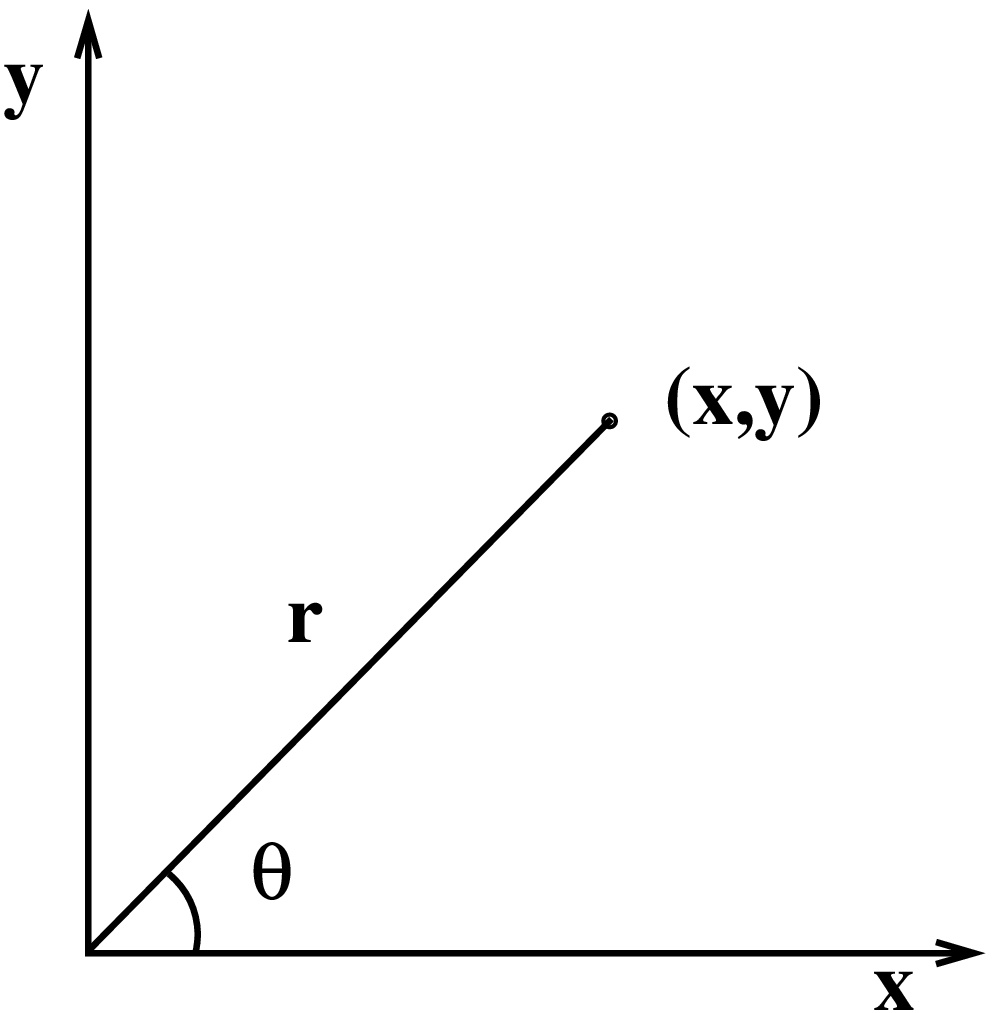
Alkeisgeometriasta saadaan kaavat \[ \left\{ \begin{array}{l} x=r\cos \theta\\ y=r\sin \theta \end{array}\right. \Leftrightarrow \left\{ \begin{array}{l} r^2=x^2+y^2 \\ \tan{\theta} = y/x. \end{array}\right. \] Vrt. kompleksiluvun polaarimuoto \(x + i y = r e^{i \theta}\).

Koordinaatistomuunnoksen \((r, \theta) \mapsto (x,y)\) Jacobin determinantille saadaan kaava \[ \frac{\partial(x,y)}{\partial (r,\theta)} = \left|\begin{array}{cc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta}\\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{array}\right| = \left|\begin{array}{cc} \cos \theta & -r\sin \theta\\ \sin \theta & r\cos\theta \end{array}\right| = r. \] Siten muuttujanvaihtokaavaa varten saadaan pinta-alan venytys \[ dx\,dy = \bigg|\frac{\partial(x,y)}{\partial (r,\theta)}\bigg| \,dr\,d\theta = r\,dr\,d\theta. \] Tasointegraali napakoordinaateissa \[ \iint_D f(x,y)\,dx\,dy = \iint_G g(r,\theta)r\,dr\,d\theta, \] missä \(g(r,\theta) = f(r\cos\theta,r\sin\theta)\).

Esimerkki

(i) Olkoon \(D=\lbrace (x,y)\in \mathbb{R}^2 : 1 < x^2 + y^2 < 4\rbrace\). Lasketaan napakoordinaateissa integraali \[ I=\iint_D \frac{1}{x^2+y^2}\,dx\,dy. \] Saadaan \[ I=\int_0^{2\pi}\int_1^2\frac{1}{r^2}r\,dr\,d\theta = \int_0^{2\pi} d\theta \cdot \int_1^2\frac{dr}{r} =2\pi\ln r\Big|_{r=1}^2 = 2\pi \ln 2. \]

(ii) Integraali \[ \int_{-\infty}^\infty e^{-x^2}\,dx \] on erittäin tärkeä mm. todennäköisyyslaskennassa ja tilastotieteessä. Tämä integraali on vaikea, koska integraalifunktiota ei ole mahdollista kirjoittaa alkeisfunktioiden avulla.

Integraali on kuitenkin mahdollista laskea seuraavan tempun avulla: Huomataan aluksi, että \[ I = \int_{-\infty}^\infty \int_{-\infty}^\infty e^{-x^2-y^2}\,dx\,dy = \bigg(\int_{-\infty}^\infty e^{-x^2}\,dx\bigg)^2. \] Laskemalla epäoleellinen tasointegraali napakoordinaateissa \[ I = \int_0^{2\pi}\int_0^\infty e^{-r^2}r\,dr\,d\theta = \int_0^{2\pi}d\theta \cdot \int_0^\infty r e^{-r^2}\,dr \] \[ = 2\pi \int_0^\infty{r e^{-r^2}\,dr} = -\pi \lim_{R \to \infty}{\int_0^R (-2r) e^{-r^2}\,dr}. \]

Nyt \(\frac{d}{dr} e^{-r^2} = -2r e^{-r^2}\), joten integraaliksi saadaan: \[ \int_0^R (-2r) e^{-r^2}\,dr = e^{-R^2} - 1 \] Viemällä \(R \to \infty\) tulee \(I = \pi\) ja siitä alkuperäisen integraalin arvo \[ \int_{-\infty}^\infty e^{-x^2}\,dx = \sqrt{I} = \sqrt{\pi}. \] Miksi temppu toimi?

Muuttujanvaihto avaruusintegraalissa

Muunnoskaavat \((u,v,w) \mapsto (x,y,z)\) ovat \[ \left\{ \begin{array}{l} x=x(u,v,w),\\ y=y(u,v,w),\\ z=z(u,v,w). \end{array}\right. \] Tällöin \[ dx\,dy\,dz = \bigg|\frac{\partial(x,y,z)}{\partial (u,v,w)}\bigg|\,du\,dv\,dw, \] missä \[ \frac{\partial(x,y,z)}{\partial (u,v,w)} = \left|\begin{array}{ccc} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} & \frac{\partial x}{\partial w} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} & \frac{\partial y}{\partial w}\\ \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} & \frac{\partial z}{\partial w} \end{array}\right|. \] Jos siis \(g(u,v,w) = f(x(u,v,w),y(u,v,w),z(u,v,w))\), niin \[ \iiint_D f(x,y,z)\,dx\,dy\,dz = \iiint_G g(u,v,w)\, \bigg|\frac{\partial(x,y,z)}{\partial (u,v,w)}\bigg|\,du\,dv\,dw. \]

Sylinterikoordinaatit

Koordinaatit \((r,\theta,z)\), missä \(r \geq 0\), \(0\le \theta<2\pi\), \(z\in\mathbb{R}\). Suoralla \(r = 0\) (eli \(z\)-akselilla) napakulma \(\theta\) ei ole yksikäsitteinen.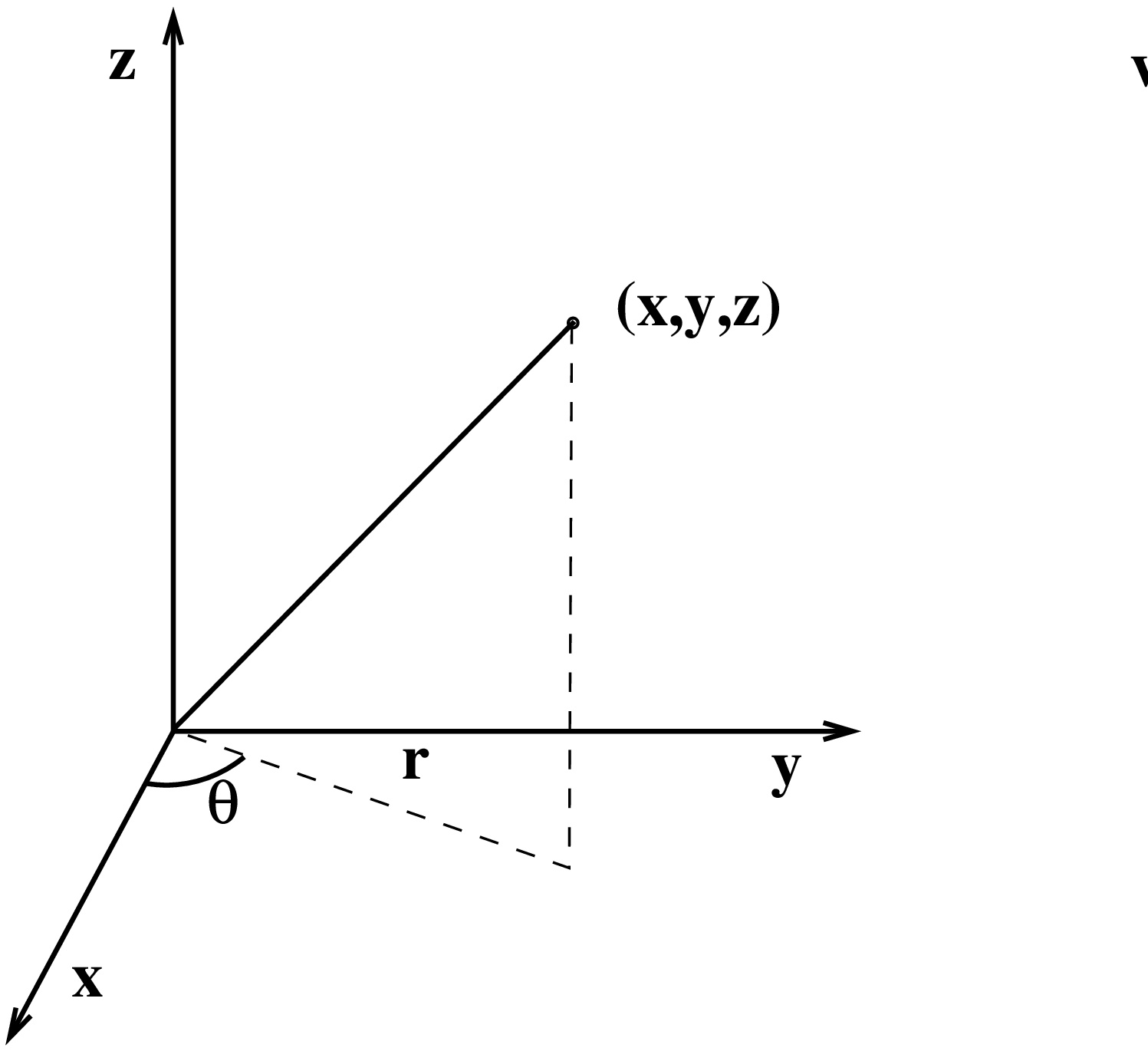

Tällöin muunnoskaavat \((r,\theta,z) \mapsto (x,y,z)\) ovat \begin{align*} \begin{cases} x &= r\cos\theta, \\ y &= r\sin\theta, \\ z &= z. \end{cases} \end{align*} Ja muunnoksen Jacobin determinantiksi saadaan \[ dx\,dy\,dz = \bigg|\frac{\partial(x,y,z)}{\partial (r,\theta,z)}\bigg|\,dr\,d\theta\,dz = r\,dr\,d\theta\,dz. \]

Sylinterikoordinaateissa on helppo esittää pyörähdyskappaleita \(z\)-akselin ympäri muodossa \[ r = f(z), \quad \text{jossa} \quad z \in [a,b] \text{ ja } \theta \in [0, 2 \pi), \] missä \(f\) on ei-negatiivinen funktio. Sylinterisymmetriset tehtävät!

Esimerkki

Lasketaan funktion \(f\) määräämän pyörähdyskappaleen \(\Omega\) tilavuus \[ \iiint_{\Omega} dx\, dy\, dz = \int_a^b\int_0^{2\pi}\int_0^{f(z)} r\,dr\,d\theta\,dz \] \[ = \int_a^b \left (2\pi \cdot \frac{1}{2}f(z)^2 \right ) \, dz = \pi \int_a^b f(z)^2 \, dz, \] mikä lienee tuttu kaava.

Pallokoordinaatit

Koordinaatit \((r,\theta,\phi)\), missä \(r \geq 0\), \(0\le \theta<2\pi\), \(0\le \phi \leq \pi\).

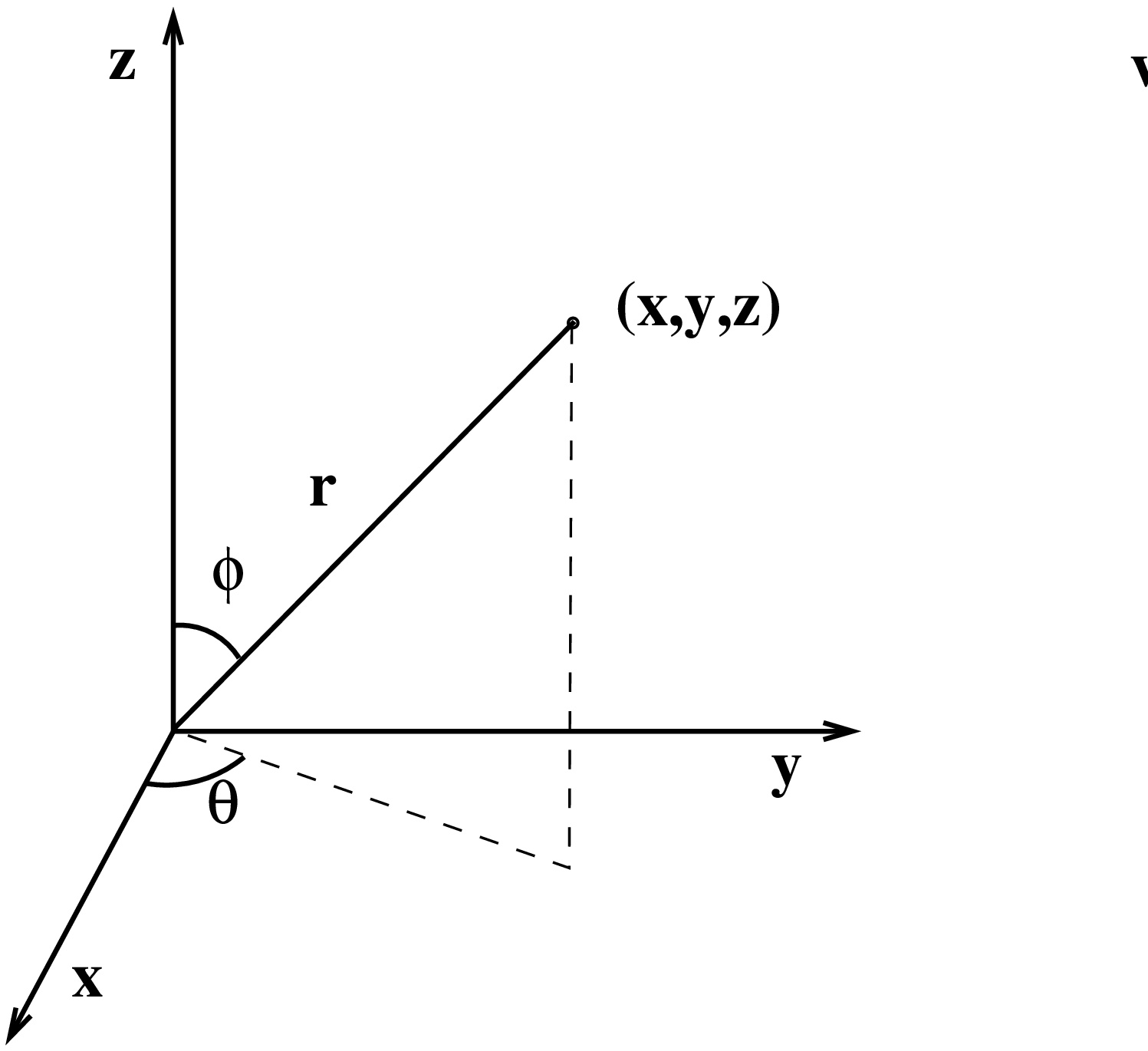
Korotus- eli napakulmaa \(\pi/2 - \phi\) käytetään usein \(\phi\):n sijasta. Atsimuuttikulma \(\theta\) ja korotuskulma ovat yksikäsitteisiä, jos pisteen etäisyys \(z\)-akselista \( > 0\). Muunnoskaavat ovat \begin{align*} \begin{cases} x&=r\sin\phi \cos\theta,\\ y&=r\sin\phi \sin\theta,\\ z&=r\cos\phi, \end{cases} \end{align*} ja muunnoksen Jacobin determinantiksi saadaan \[ dx\,dy\,dz = \bigg|\frac{\partial(x,y,z)}{\partial (r,\theta,\phi)}\bigg|\,dr\,d\theta\,d\phi = r^2\sin\phi \,dr\,d\theta\,d\phi. \]

Esimerkki

Lasketaan \(R\)-säteisen pallon \(\mathbb{B}^3(R)\) tilavuus: \[ V(\mathbb{B}^3) = \iiint_{\mathbb{B}^3(R)} 1\,dx\,dy\,dz = \int_0^R\int_0^{2\pi}\int_0^\pi r^2\sin\phi\,d\phi\,d\theta\,dr \] \[ = \int_0^R\int_0^{2\pi} -r^2\cos\phi\bigg|_{\phi=0}^\pi\,d\theta\,dr = \int_0^R\int_0^{2\pi} 2r^2\,d\theta\,dr \] \[ =\int_0^R 4\pi r^2\,dr = \frac{4\pi r^3}{3}\bigg|_{r=0}^R = \frac{4\pi R^3}{3}. \]

Kaksiulotteinen pinta-ala avaruudessa

Tutkitaan kaksiulotteista kaareutuvaa pintaa \(S\), joka on (piirtämisen helpottamiseksi) \(xy\)-tason yläpuolella avaruudessa \(\mathbb{R}^3\).

Tarkastellaan aluksi \(xy\)-tason neliön yläpuolelle jäävän osan pinta-alaa. Se on ilmeisesti suurempi tai yhtäsuuri kuin vastaavan neliön pinta-ala.

Tästä johtuen pinta-aladifferentiaali \(dS\) on suurempi tai yhtäsuuri kuin kuin \(dx\,dy\). Itseasiassa \(dx\,dy\) saadaan, jos \(dS\) projisoidaan \(xy\)-tasoon. Projektio voidaan kirjoittaa kaavana \[ dx\,dy = \cos \gamma\,dS, \] missä \(\gamma\) on pinnan \(S\) normaalivektorin \(\mathbf{N}\) ja \(z\)-akselin suuntaisen yksikkövektorin \(\mathbf{k}\) välinen kulma. Toisaalta pistetulon määritelmästä saadaan \[ \mathbf{N} \cdot \mathbf{k} = \|\mathbf{N}\| \|\mathbf{k}\| \cos \gamma, \] ja siis \[ dS = \frac{1}{\cos \gamma}\,dx\,dy = \frac{\|\mathbf{N}\| \|\mathbf{k}\|}{\mathbf{N} \cdot \mathbf{k}}\,dx\,dy. \]

Aikaisemmin on johdettu pinnan (ylöspäin suunnatulle) normaalivektorille esitys \[ \mathbf{N} = -\frac{\partial z}{\partial x}\mathbf{i} - \frac{\partial z}{\partial y}\mathbf{j} + \mathbf{k}. \] Saadaan \[ \|\mathbf{N}\| = \sqrt{1+ \Big(\frac{\partial z}{\partial x}\Big)^2 + \Big(\frac{\partial z}{\partial y}\Big)^2} \] Lisäksi \(\|\mathbf{k} \| =1\) ja \(\mathbf{N}\cdot \mathbf{k} = 1\), joten \[ dS = \sqrt{1+ \Big(\frac{\partial z}{\partial x}\Big)^2 + \Big(\frac{\partial z}{\partial y}\Big)^2}\,dx\,dy. \] Kaltevuuden huomioiva korjaustekijä yleistää tasointegraalin pintaintegraaliksi.

Esimerkki

Tarkastellaan sylinterin \(x^2+y^2=a^2\), \(a>0\) leikkaamaa palasta hyperbolisesta paraboloidista \(z=x^2-y^2\). Mikä on palasen pinta-ala?

Lasketaan \[ \frac{\partial}{\partial x} z = 2x,\qquad \frac{\partial}{\partial y} z = -2y. \] Siten pinta-aladifferentiaaliksi saadaan \[ dS = \sqrt{1+ \Big(\frac{\partial z}{\partial x}\Big)^2 + \Big(\frac{\partial z}{\partial y}\Big)^2}\,dx\,dy \] \[ = \sqrt{ 1 + 4(x^2+y^2)} \,dx\,dy \] \[ =\sqrt{1+ 4r^2}\, r\,dr\,d\theta, \] napakoordinaateissa ilmaistuna.

Lasketaan nyt integraali napakoordinaateissa: \[ \textrm{Ala}(S)= \int_0^{2\pi} \int_0^a r\sqrt{1+4r^2}\,dr\,d\theta \] \[ = \frac{\pi}{4} \int_0^a 8r\sqrt{1+4r^2}\,dr \] \[ = \frac{\pi}{4} \bigg|_{r=0}^a\frac{2}{3}(1+4r^2)^{3/2} =\frac{\pi}{6} \big[(1+4a^2)^{3/2} -1\big]. \]