Differentiaali- ja integraalilaskenta 2, kevät 2022 (Aalto MOOC)

Epäoleelliset integraalit

Tähän asti integrointi on tapahtunut rajoitetussa alueessa rajoitetulle funktiolle (integrandille). Joskus voidaan kuitenkin integroida rajoittamattomia funktioita ja/tai rajoittamattomassa alueessa.

Tarkastellaan ainoastaan tapausta, jossa funktio \(f\) on ei-negatiivinen eli \(f(\mathbf{u}) \ge 0\) kaikilla \(\mathbf{u}\in D\). Lasketaan funktion \(f(x,y) = e^{-x^2}\) integraali alueessa suorien \(y=\pm x\) rajoittamassa rajoittamattomassa alueessa \(D\), jossa \(x>0\). Mikäli integraali on suppenee, sen arvo saadaan laskemalla \[ \iint_D e^{-x^2}\,dA = \int_0^\infty \int_{-x}^{x} e^{-x^2}\,dy\,dx = \int_0^\infty 2xe^{-x^2}\,dx \] \[ = \lim_{R\to \infty} \int_0^R 2xe^{-x^2}\,dx. \] Integraalin laskemiseksi huomataan, että \(\frac{d}{dx} e^{-x^2} = -2xe^{-x^2}\). Siten \[ \lim_{R\to \infty} \int_0^R 2xe^{-x^2}\,dx = \lim_{R\to\infty} -e^{-x^2}\Big|_{x=0}^R = \lim_{R\to\infty}1-e^{-R^2}=1. \]

Esimerkki

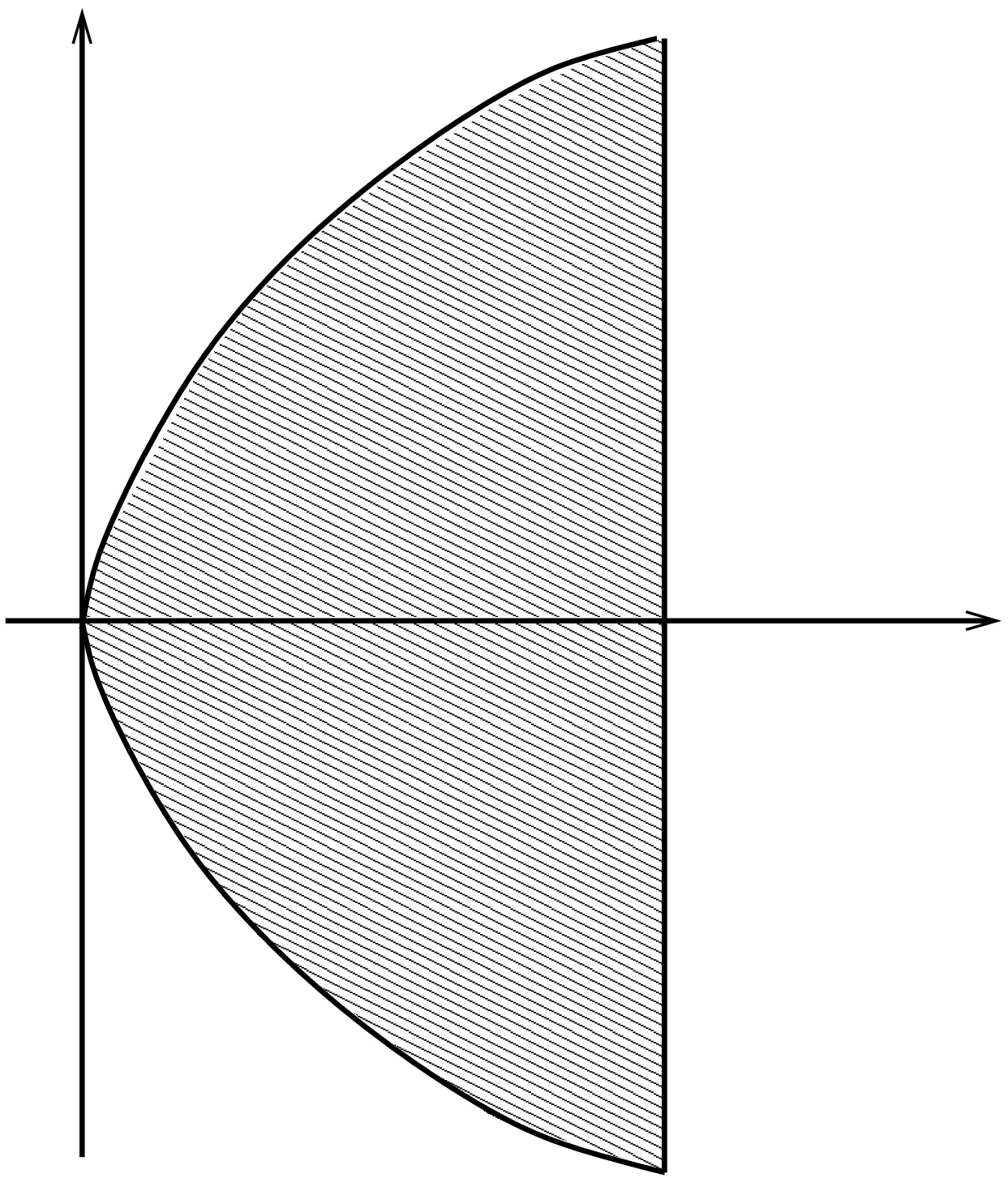
Olkoon \[D_1=\lbrace (x,)\in \mathbb{R}^2 : 0 < x < 1, \, |y| \leq x^2 \rbrace\] ja rajoittamaton funktio \(f(x,y)=1/x^2\).

(i) Lasketaan integraali \[ \iint_{D_1}\frac{1}{x^2}\,dA =\int_0^1\int_{-x^2}^{x^2}\frac{1}{x^2}\,dy\,dx \] \[ =\int_0^1 2\,dx =2. \]

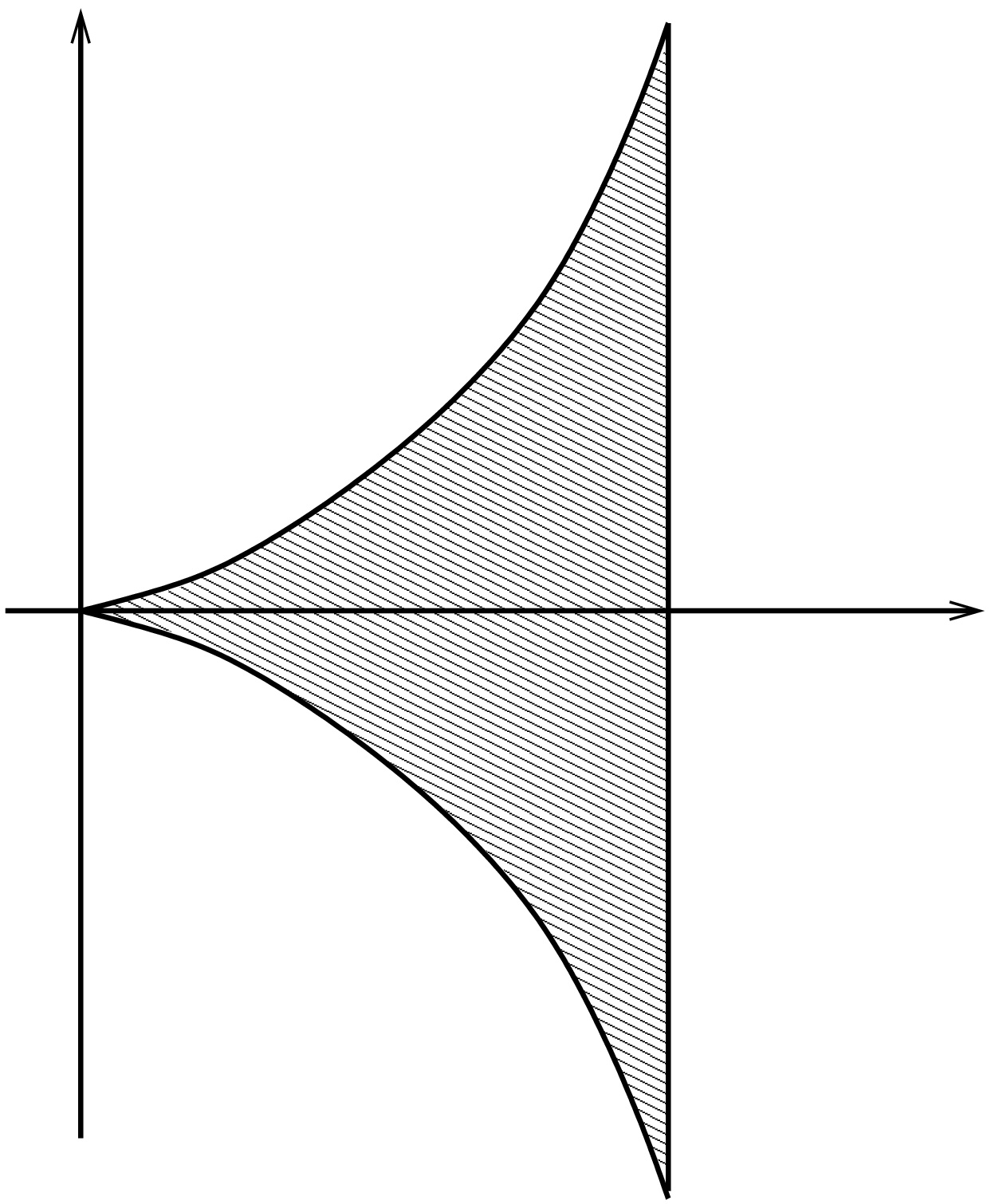
(ii) Lasketaan saman funktion integraali alueessa \[D_2=\lbrace (x,y)\in\mathbb{R}^2 : 0 < x < 1,\, |y|\leq \sqrt{x}\rbrace.\] \[ \iint_{D_2}\frac{1}{x^2}\,dA =\int_0^1\int_{-\sqrt{x}}^{\sqrt{x}}\frac{1}{x^2}\,dy\,dx \] \[ =\int_0^1 2\sqrt{x}\frac{1}{x^2}\,dx =\int_0^1 2x^{-3/2}\,dx =\lim_{\epsilon\to 0+} \frac{2x^{-1/2}}{-1/2}\bigg|_{x=\epsilon}^1 = \infty. \] Suppeneminen riippuu integroitavan funktion lisäksi myös alueesta!

Muuttujanvaihto taso- ja avaruusintegraaleissa

Tutkitaan funktiota \(\mathbf{F}\colon G \to D\), missä \(D\) ja \(G\) ovat \(\mathbb{R}^2\):n osajoukkoja. Oletetaan, että funktion \(\mathbf{F}\) kaikki osittaisderivaatat ovat olemassa ja jatkuvia. Lisäksi oletetaan, että \(\mathbf{F}\) on bijektio: Jokaista pistettä \((x,y) \in D\) vastaa yksikäsitteinen piste \((u,v)\in G\), jolle \(\mathbf{F}(u,v)= (x,y)\). Tällöin erityisesti \(D=\mathbf{F}(G)\).

 

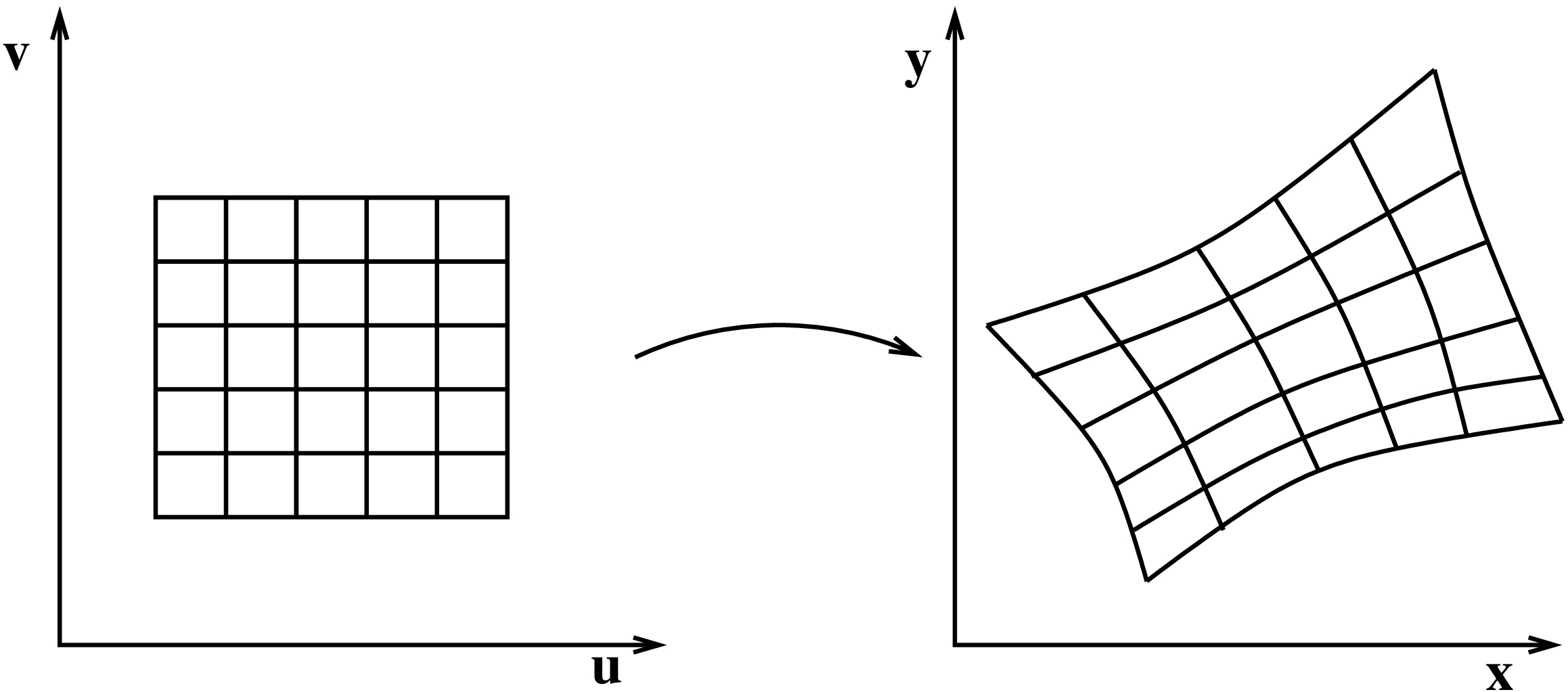
Tutkitaan aluksi muuttujanvaihtoa tasointegraalin tapauksessa: \[ \iint_D f(x,y)\,dx\,dy = \iint_{G} ??? \,du\,dv. \] Tarvitaan tieto siitä, miten pinta-ala skaalautuu funktiossa \((x,y) = \mathbf{F}(u,v)\).

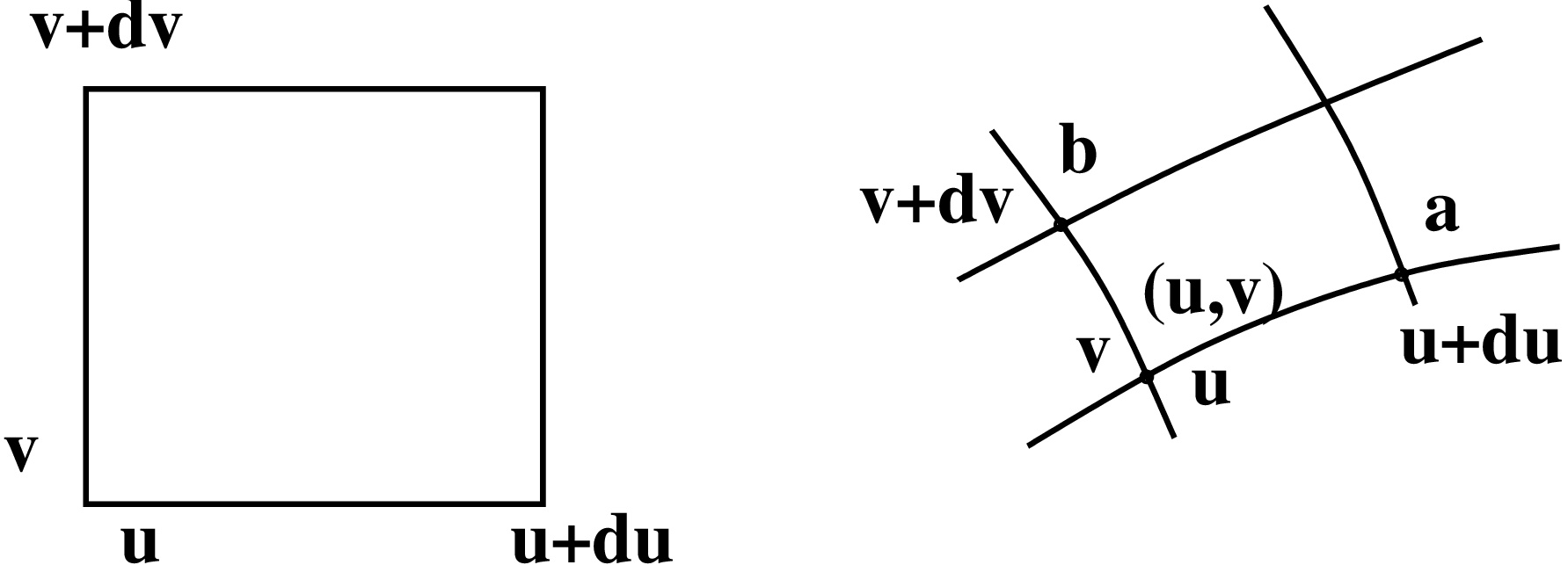
Ketjusäännöllä \[ dx = \frac{\partial x}{\partial u}du + \frac{\partial x}{\partial v}dv\text{ ja } dy = \frac{\partial y}{\partial u}du + \frac{\partial y}{\partial v}dv. \] Edettäessä vektorin \(\mathbf{a}\) suuntaan \((x,y)\)-koordinaateissa, koordinaatti \(v\) on vakio ja siten \(dv=0\). Saadaan \[ \mathbf{a} \approx \frac{\partial x}{\partial u}du\,\mathbf{i} + \frac{\partial y}{\partial u}du\,\mathbf{j}. \] Samaan tapaan voidaan päätellä, että \[ \mathbf{b} \approx \frac{\partial x}{\partial v}dv\,\mathbf{i} + \frac{\partial y}{\partial v}dv\,\mathbf{j}. \] Tässä \(\mathbf{i}\) ja \(\mathbf{j}\) ovat koordinaattiakseleiden suuntaiset yksikkövektorit.

Approksimaatiokaava pinta-alaelementin \(dA\) muutokselle siis on \[ dA = dx \, dy \approx |\mathbf{a} \times \mathbf{b}| = \left\|\begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial x}{\partial u}du & \frac{\partial y}{\partial u}du & 0 \\ \frac{\partial x}{\partial v}dv & \frac{\partial y}{\partial v}dv & 0 \end{array}\right\| \] Käytetään merkintää (huom. neliömatriiseille \(\det A=\det A^T\)) \[ \left\|\begin{array}{cc} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{array}\right\|\,du\,dv := \big|\det D \mathbf{F}(u,v)\big|\,du\,dv. \] Determinantti \(\det D \mathbf{F}(u,v)\) on funktion \(\mathbf{F}\colon \mathbb{R}^2\to \mathbb{R}^2\) Jacobin determinantti. Sille käytetään myös merkintää \[ \det D \mathbf{F}(u,v)=\frac{\partial(x,y)}{\partial(u,v)} \text{ kun } (x,y) = \mathbf{F}(u,v). \]

Jacobin determinantin itseisarvo \(|\det D \mathbf{F}(u,v)|\) kertoo paikallisen pinta-alan muutoksen kuvattaessa \((u,v)\)-koordinaattien infinitesimaalinen pinta-ala \(du\,dv\) vastaavalle \((x,y)\)-koordinaateissa lausutulle pinta-alalle \(dx\,dy\) funktion \((x,y) = \mathbf{F}(u,v)\) välityksellä.

Tasointegraalin muuttujanvaihtokaavaksi siis saadaan \[ \iint_D f(x,y) \,dx\,dy = \iint_{G} g(u,v) \big | \det D\mathbf{F} (u,v)\big| \,du\,dv \] missä \(g(u,v)=f(x(u,v),y(u,v))\) ja \(D=\mathbf{F}(G)\). Tässä \(\mathbf{F}\) on integroimisalueiden \(D\) ja \(G\) välinen bijektio. Jacobin determinantin etumerkki kertoo, onko \(\mathbf{F}\) suunnan säilyttävä vai kääntävä. Itseisarvo tarvitaan, jotta positiivisen funktion integraali ei muuttuisi negatiiviseksi eräillä \(\mathbf{F}\).

Esimerkki

Lasketaan neljän paraabelin \(y=x^2\), \(y=2x^2\), \(x=y^2\) ja \(x=3y^2\) rajoittamaan alueen \(D\) pinta-ala.

Huomataan, että integroimisalue kuvautuu suorakulmioksi \(G = [1/2 , 1] \times [1/3 , 1]\) muunnoksella \[ \mathbf{G}(x,y) = u\mathbf{i} + v\mathbf{j}, \quad u(x,y)=\frac{x^2}{y},\,\,v(x,y)=\frac{y^2}{x}. \]

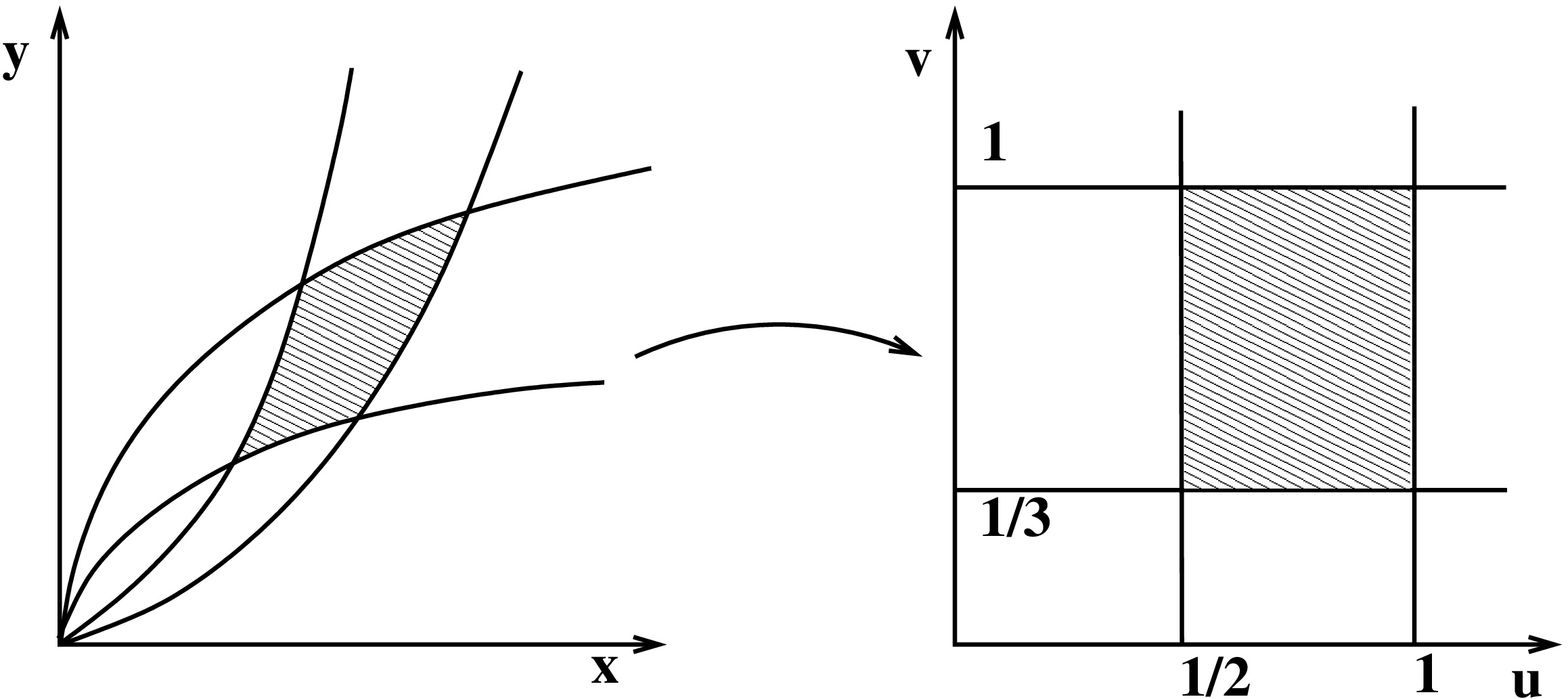
Halutaan kuitenkin käänteiskuvaus \(\mathbf{F} = \mathbf{G}^{-1}\colon G\to D\), joka vie koordinaatit \((u,v)\) käyräviivaisille \((x,y)\)-koordinaateille. Lineaarialgebran perusteella \[ \det D {{\mathbf{F}}}(u,v)=\frac{1}{\det D \mathbf{G}(x,y)}. \] Lasketaan \[ \frac{\partial u}{\partial x} = \frac{2x}{y}, \quad \frac{\partial u}{\partial y} = -\frac{x^2}{y^2}. \] Saadaan myös \[ \frac{\partial v}{\partial x} = -\frac{y^2}{x^2}, \quad \frac{\partial v}{\partial y} = \frac{2y}{x}. \]

Lasketaan edelleen \[ \det D \mathbf{G}(x,y) = \left|\begin{array}{cc} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} \end{array}\right| = \left|\begin{array}{cc} \frac{2x}{y} & -\frac{x^2}{y^2} \\ -\frac{y^2}{x^2} & \frac{2y}{x} \end{array}\right| \] \[ = 4-1 = 3,\text{ eli } \big|\det D {\mathbf{F}} (u,v)\big|=\frac{1}{3}. \] Tulokseksi siis saadaan \[ \iint_D 1\,dx\,dy = \iint_G \frac{1}{3}\,du\,dv = \frac{1}{3}\cdot \frac{2}{3}\cdot \frac{1}{2} = \frac{1}{9}. \] Yleensä ei käy niin onnellisesti, että sama koordinaatistomuunnos vie integroitavan alueen suorakulmiolle samalla kun integroitava funktio menee vakioksi.