Föregående
Nästa

6. Ääriarvojen luokittelu

Kertausta: ääriarvot yhden muuttujan tapauksessa

Funktiolla \(f\colon I\subset \mathbb{R} \to \mathbb{R}\) on lokaali (paikallinen) maksimi pisteessä \(a\in I\), jos \(f(x)\le f(a)\) kaikilla \(x\):n arvoilla jossakin \(a\):n ympäristössä (eli riittävän lähellä pistettä \(a\)). Vastaavasti lokaali minimi tarkoittaa sitä, että \(f(x)\ge f(a)\) jossakin \(a\):n ympäristössä. Maksimi tai minimi on globaali, jos kyseinen epäyhtälö on voimassa kaikilla \(x\in I\).
Ääriarvoja voi esiintyä:
  1. Funktion \(f\) kriittisissä pisteissä, joissa \(f'(x)=0\),
  2. pisteissä joissa \(f\):n derivaatta ei ole määritelty, ja
  3. määrittelyjoukon \(I\) reunalla.

Seuraavaksi yleistetään vastaavat ehdot funktion \(f\colon D\subset \mathbb{R}^n\to\mathbb{R}\) tapaukseen.

Ääriarvot ja usean muuttujan funktiot

Funktiolla \(f\colon D\subset \mathbb{R}^n\to\mathbb{R}\) on pisteessä \(\mathbf{x}_0\in D\) lokaali maksimi, jos jossakin pisteen \(\mathbf{x}_0\) ympäristössä \(U\subset D\) pätee \(f(\mathbf{x})\le f(\mathbf{x}_0)\) kaikilla \(\mathbf{x}\in U\). Vastaavasti \(f\colon D\subset \mathbb{R}^n\to\mathbb{R}\) on pisteessä \(\mathbf{x}_0\in D\) lokaali minimi, jos löytyy sellainen pisteen \(\mathbf{x}_0\) ympäristö \(U\subset D\), että \(f(\mathbf{x})\ge f(\mathbf{x}_0)\) kaikilla \(\mathbf{x}\in U\). Ääriarvo on globaali eli absoluuttinen, jos kyseinen epäyhtälö on voimassa kaikilla \(\mathbf{x}\in D\).
Ääriarvoja voi esiintyä:
  1. Funktion \(f\) kriittissä pisteissä eli gradientin nollakohdissa \(\nabla f(\mathbf{x})=0\),
  2. pisteissä joissa \(\nabla f\) ei ole määritelty, sekä
  3. määrittelyjoukon \(D\) reunalla.
Joukon \(D\) kriittistä pistettä \(\mathbf{x}_0\), joka ei ole maksimi tai minimi, kutsutaan funktion \(f\colon D\to \mathbb{R}\) satulapisteeksi.
Esimerkki
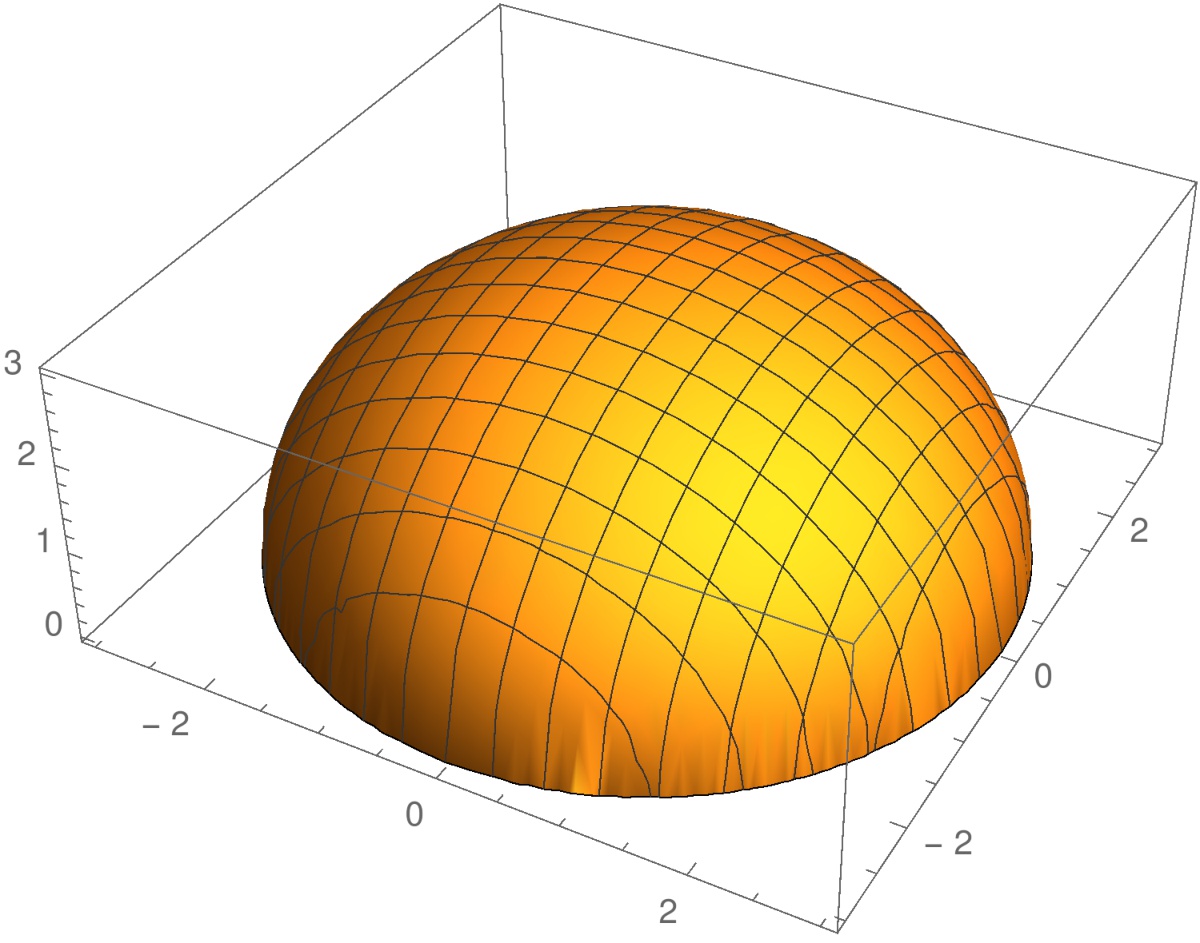
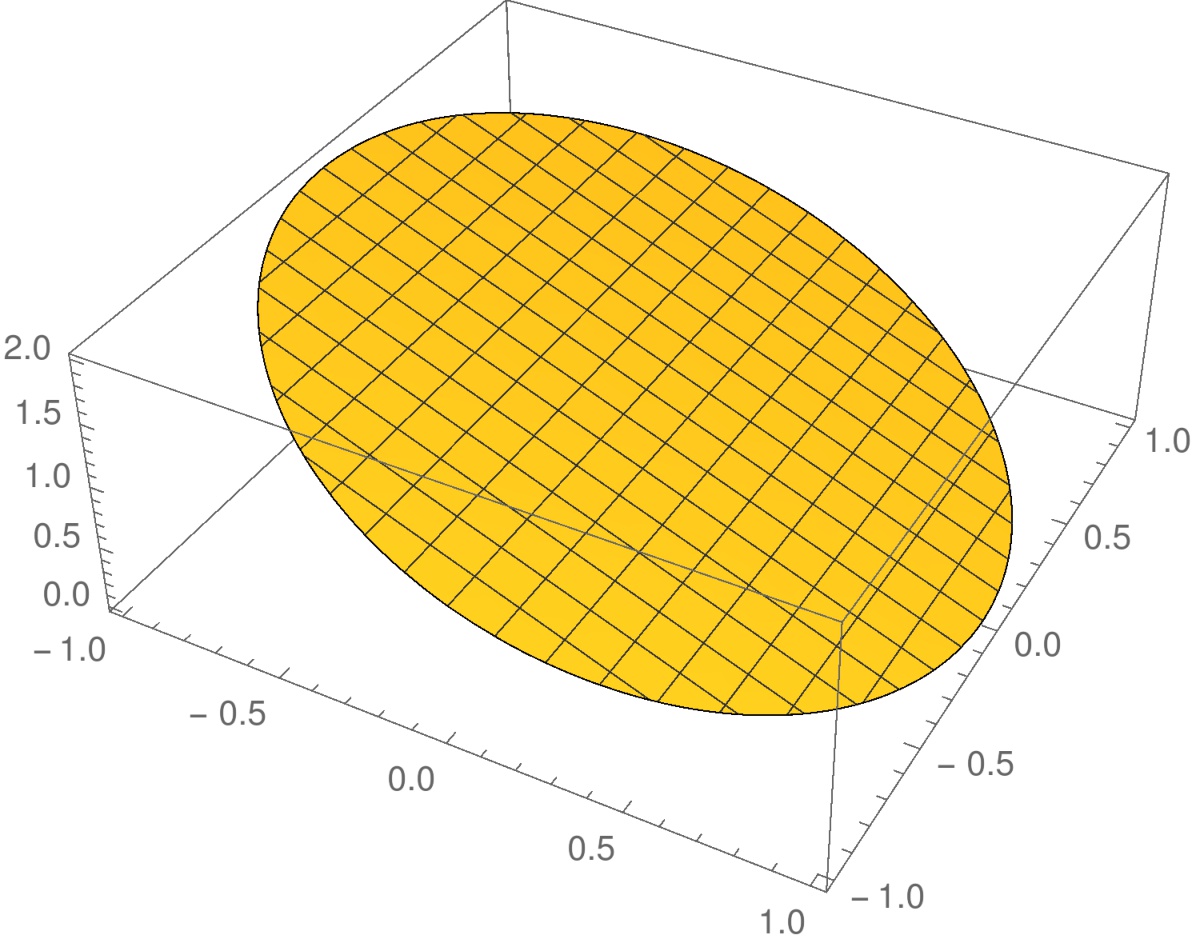
funktion kuvaaja

Funktiolla \(f(x,y)= 1-x^2-y^2\) on globaali maksimi \(f(0,0)=1\) pisteessä \((0,0)\). Tämä piste on funktion \(f\) kriittinen piste, koska \[ \nabla f(0,0) = -2x\mathbf{i} -2y\mathbf{j} \Big|_{(0,0)}= \mathbf{0}. \]

Esimerkki
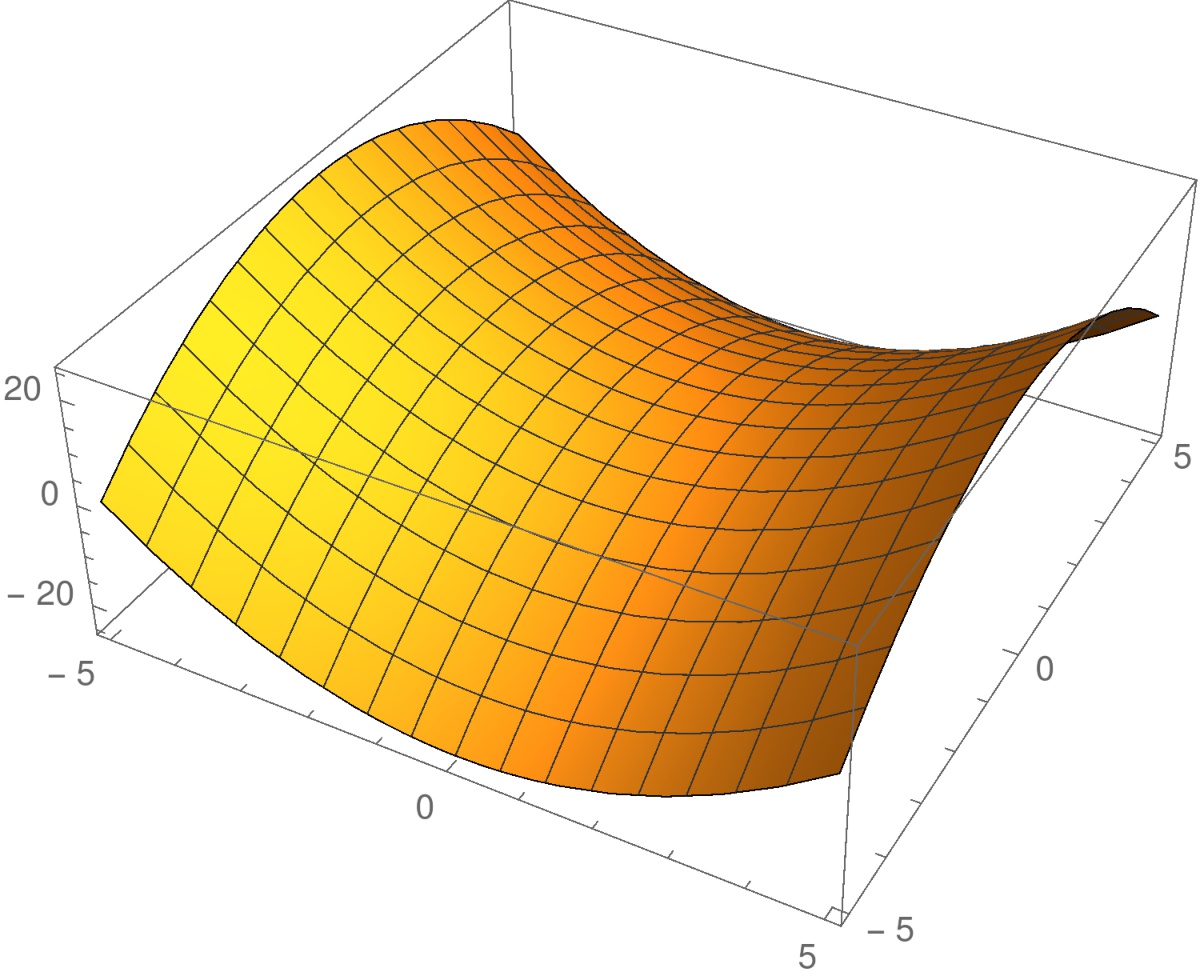
funktion kuvaaja
Funktiolla \(f(x,y)= y^2-x^2\) on satulapiste \((0,0)\). Tämä piste on funktion \(f\) kriittinen piste, koska \[ \nabla f(0,0) = -2x\mathbf{i}+2y\mathbf{j}\Big|_{(0,0)}= \mathbf{0}. \]
Esimerkki
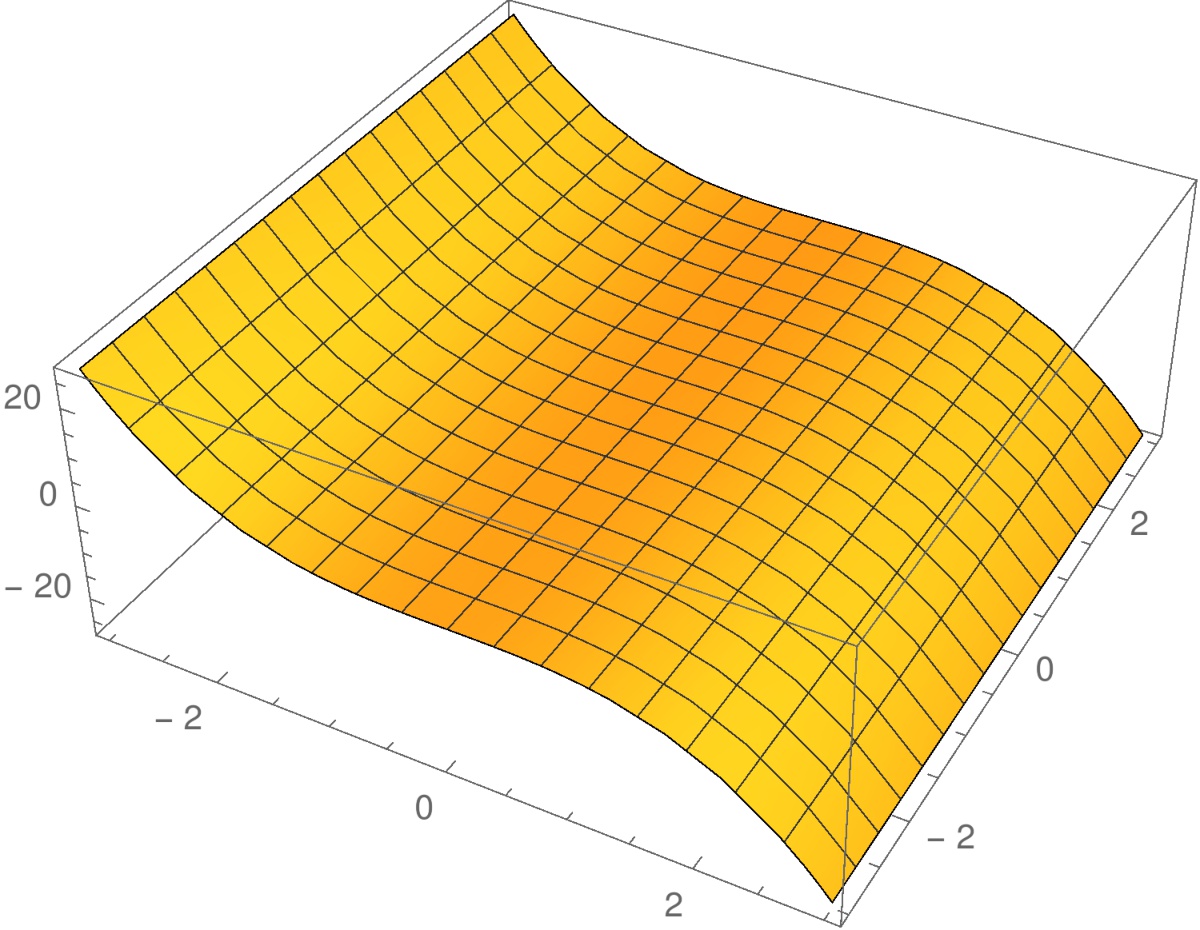
funktion kuvaaja
Kaikki pisteet suoralla \(x=0\) ovat funktion \(f(x,y)= -x^3\) satulapisteitä. Huomaa, että \[ \nabla f(0,y) = -3x^2\mathbf{i} \Big|_{(0,y)}= \mathbf{0} \text{ kaikilla }y\in \mathbb{R}. \]
Esimerkki
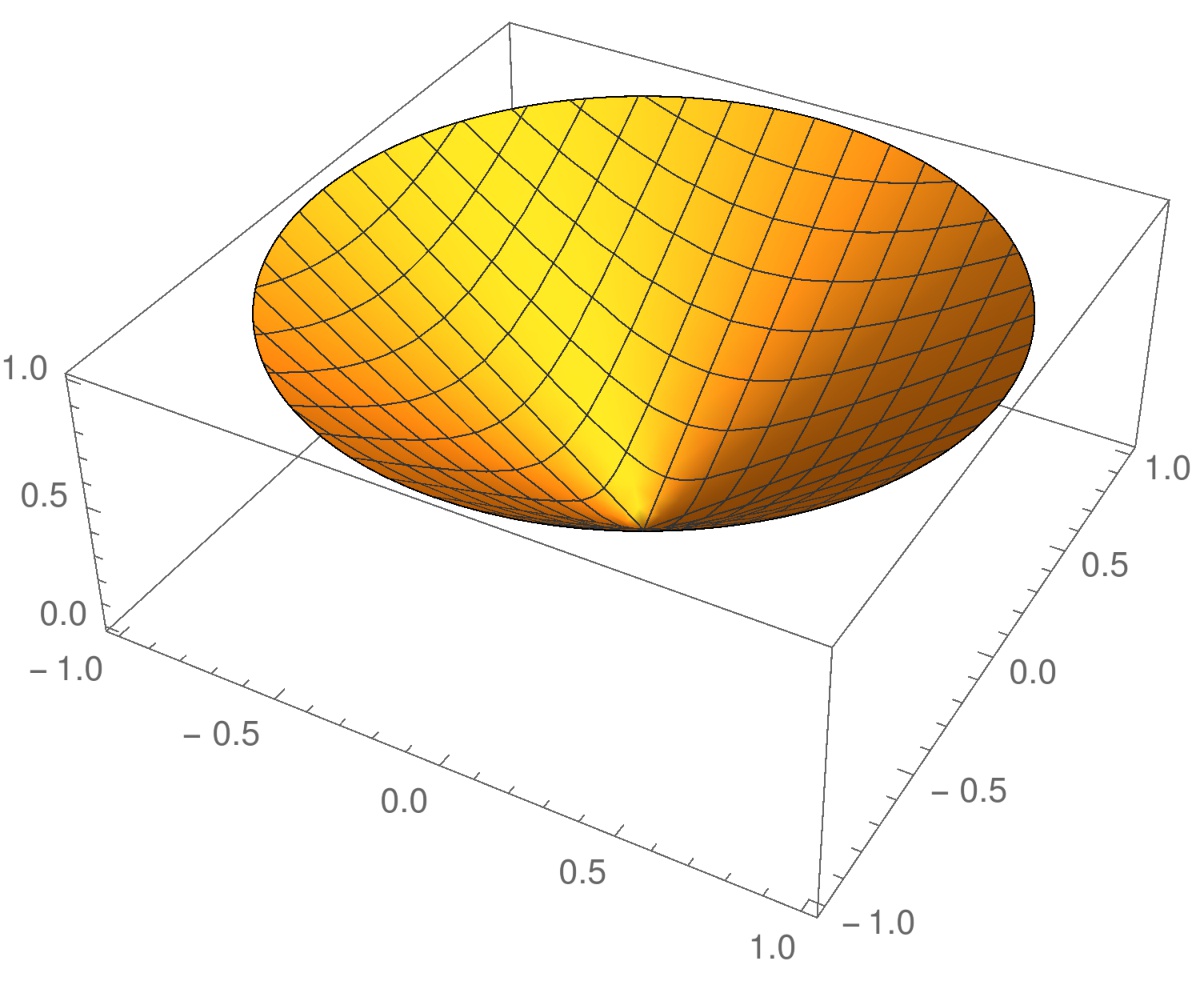
funktion kuvaaja
Funktiolla \(f(x,y)= \sqrt{x^2+y^2}\) on lokaali minimi \(f(0,0)=0\) pisteessä \((0,0)\). Funktio \(f\) on jatkuva, mutta sen gradientti \(\nabla f\) ei ole määritelty tässä pisteessä.
Esimerkki
funktion kuvaaja
Funktiolla \(f(x,y)=1-x\) ei ole paikallisia ääriarvoja, jos sen määrittelyjoukko on koko taso \(D=\mathbb{R}^2\). Jos määrittelyjoukoksi kuitenkin ajatellaan esimerkiksi kiekko \(D=\{(x,y): x^2+y^2 \leq 1\}\), niin sen reunalla saadaan maksimi \(f(-1,0)=2\) ja minimi \(f(1,0)=0\).

Ääriarvojen luokittelu: johdanto

Ääriarvojen luokittelu perustuu suureen \(\Delta f= f(\mathbf{x} + \mathbf{h}) -f(\mathbf{x})\) tarkasteluun kriittisessä pisteessä \(\mathbf{x}\in D\). Jos \(\Delta f\) saa vain positiivisia arvoja (kun \(\|\mathbf{h}\|\) on pieni), on piste \(\mathbf{x}\) minimi ja negatiivisessa tapauksessa maksimi. Jos \(\Delta f\) vaihtaa merkkiä, niin piste \(\mathbf{x}\) ei ole minimi eikä maksimi. Tämä johtaa funktion \(f\) toisen derivaatan tarkasteluun kriittisessä pisteessä.
Yhden muuttujan tapauksessa:
  1. Jos \(f''(x)< 0\), niin funktiolla \(f\) lokaali maksimi pisteessä \(x\).
  2. Jos \(f''(x)>0\), niin funktiolla \(f\) lokaali minimi pisteessä \(x\).
  3. Jos \(f''(x)=0\), niin testi ei anna vastausta, ja kysymys täytyy ratkaista muulla tavoin.
Seuraavaksi yritetään yleistää tätä ajatusta monen muuttujan funktiolle.

Hessen matriisi

Olkoon \(f\colon D\subset \mathbb{R}^n \to \mathbb{R}\) funktio, jolla on jatkuvat toisen kertaluvun osittaisderivaatat. Funktion \(f\) luonnollinen derivaattakäsite on gradientti, joka itsessään on vektoriarvoinen funktio \(\nabla f\colon \mathbb{R}^n \to \mathbb{R}^n\). Siten funktion \(f\) toinen derivaatta on matriisi, jota nimitetään Hessen matriisiksi \[ H_f(\mathbf{x})= \begin{bmatrix} \frac{\partial^2}{\partial x_1^2} f(\mathbf{x}) & \frac{\partial^2}{\partial x_2\partial x_1} f(\mathbf{x}) & \cdots & \frac{\partial^2}{\partial x_n\partial x_1} f(\mathbf{x})\\ \frac{\partial^2}{\partial x_1\partial x_2} f(\mathbf{x}) & \frac{\partial^2}{\partial x_2^2} f(\mathbf{x}) & \cdots & \frac{\partial^2}{\partial x_n\partial x_2} f(\mathbf{x})\\ \vdots & \vdots & & \vdots \\ \frac{\partial^2}{\partial x_1\partial x_n} f(\mathbf{x}) & \frac{\partial^2}{\partial x_2\partial x_n} f(\mathbf{x}) & \cdots & \frac{\partial^2}{\partial x_n^2} f(\mathbf{x}) \\ \end{bmatrix}. \] Koska \(f\) on kaksi kertaa jatkuvasti derivoituva, derivoinnin järjestystä voidaan vaihtaa, ja kyseinen matriisi on symmetrinen.

Miksi Hessen matriisi kiinnostaa meitä? Kun gradientin avulla voidaan kirjoittaa lineaarinen (ensimmäisen asteen) approksimaatio funktiolle \(f\), niin Hessen matriisilla saadaan kvadraattinen tarkennus: \[ f(\mathbf{x} + \mathbf{h}) \approx f(\mathbf{x}) + \mathbf{h} \cdot \nabla f (\mathbf{x}) + \frac{1}{2} \mathbf{h} H_f(\mathbf{x}) \mathbf{h}^T, \] jossa (vaaka)vektori \(\mathbf{h} = (h_1, h_2, \ldots , h_n)\) on pieni.

Tämä kaava on itse asiassa ainoastaan uusi tapa kirjoittaa toisen kertaluvun Taylorin approksimaatio \(n\):n muuttujan funktiolle. Muotoa \(\mathbf{z} ^T A \mathbf{z}\) oleva lauseke on \(n\times n\)-neliömatriisille \(A\) niin kutsuttu neliömuoto, jossa \(\mathbf{z}\) on \(n\)-pystyvektori.

Kirjoita kaava auki tapauksessa \(n = 2\)!

Pisteessä, jossa \(\nabla f (\mathbf{x}) = 0\), on voimassa approksimaatio \[f(\mathbf{x} + \mathbf{h}) - f(\mathbf{x}) \approx \frac{1}{2} \mathbf{h} H_f(\mathbf{x}) \mathbf{h}^T.\] Tätä voidaan käyttää hyväksi mahdollisen ääriarvon luokittelussa pisteessä \(\mathbf{x}\) ajattelemalla, että \(\mathbf{h} \approx 0\).

Matriisin (ja neliömuodon) definiittisyys

Symmetristä \(n\times n\)-matriisia \(A\) sanotaan positiividefiniitiksi, jos sen kaikki ominaisarvot ovat positiivisia ja negatiividefiniitiksi, jos \(-A\) on positiividefiniitti. Matriisin sanotaan olevan indefiniitti, jos sen kaikki ominaisarvot ovat nollasta poikkeavia ja sillä on vähintään yksi positiivinen sekä yksi negatiivinen ominaisarvo. Positiivi/negatiividefiniiteillä matriiseilla on monia samoja ominaisuuksia kuin positiivisilla/negatiivisilla reaaliluvuilla.

Symmetrisen matriisin \(A\) definiittiys tai indefiniittiys periytyy sitä vastaavalle neliömuodolle.
\(A\) on positiividefiniitti \(\Leftrightarrow\) \(\mathbf{x}^T A \mathbf{x}>0\) kaikilla nollasta poikkeavilla pystyvektoreilla \(\mathbf{x}\in \mathbb{R}^n\).
\(A\) on negatiividefiniitti \(\Leftrightarrow\) \(\mathbf{x}^T A \mathbf{x}< 0\) kaikilla nollasta poikkeavilla pystyvektoreilla \(\mathbf{x}\in \mathbb{R}^n\).
\(A\) on indefiniitti \(\Leftrightarrow\) \(\mathbf{x}^T A \mathbf{x}\) saavuttaa sekä negatiivisia että positiivisia arvoja pystyvektorin \(\mathbf{x}\) vaihdellessa.

Väite nähdään todeksi ortogonaalidiagonalisoimalla symmetrinen matriisi \(A\) muotoon \(A = U^T \Lambda U\), jossa diagonaalimatriisi \(\Lambda\) sisältää \(A\):n ominaisarvot.

Toisen derivaatan testi monen muuttajan tapauksessa

Lause. Olkoon \(f\colon D\subset \mathbb{R}^n\to\mathbb{R}\) funktio, jolla on jatkuvat toisen kertaluvun osittaisderivaatat kriittisen pisteen \(\mathbf{x}\in D\) ympäristössä. Tällöin:
  1. Jos \(H_f(\mathbf{x})\) on positiividefiniitti, niin \(f\):llä on lokaali minimi pisteessä \(\mathbf{x}\).
  2. Jos \(H_f(\mathbf{x})\) on negatiividefiniitti, niin \(f\):llä on lokaali maksimi pisteessä \(\mathbf{x}\).
  3. Jos \(H_f(\mathbf{x})\) on indefiniitti, niin \(\mathbf{x}\) on funktion \(f\) satulapiste.
  4. Muussa tapauksessa testi ei anna tietoa funktiosta \(f\).

Lause seuraa approksimaatiosta \(f(\mathbf{x} + \mathbf{h}) - f(\mathbf{x}) \approx \frac{1}{2} \mathbf{h} H_f(\mathbf{x}) \mathbf{h}^T\) kun \(\mathbf{h} \approx 0\). Väite täytyy nimittäin ainoastaan tarkastaa Hessen matriisin määräämälle neliömuodolle.

Esimerkki

Etsitään ja luokitellaan funktion \[ f(x,y,z) = x^2y+y^2z+z^2-2x \] kriittiset pisteet.

Yhtälöt kriittisille pisteille ovat \begin{align*} 0 &= f_{x}(x,y,z)=2xy-2,\\ 0 &= f_{y}(x,y,z)=x^2+2yz,\\ 0 &= f_{z}(x,y,z)=y^2+2z.\\ \end{align*} Nämä yhtälöt ratkaisemalla nähdään, että funktion \(f\) ainoa kriittinen piste on \(P=(1,1,-1/2)\).

Lasketaan Hessen matriisi \[H_f(1,1,-1/2)=\left [ \begin{smallmatrix} 2 & 2 & 0 \\ 2 & -1 & 2 \\ 0 & 2 & 2 \end{smallmatrix} \right ]\] ja lasketaan matriisin ominaisarvot vaikkapa MATLABilla

   >> a = [2 2 0 ; 2 -1 2 ; 0 2 2]
   a =
       2     2     0
       2    -1     2
       0     2     2
   >> eig(a)
   ans =
      -2.7016
       2.0000
       3.7016

Niinpä funktiolla \(f\) on satulapiste pisteessä \(P=(1,1,-1/2)\).

Föregående
Nästa