Differential and Integral Calculus 2021
7. Area
Table of Content
Area in the plane
We consider areas of plane sets bounded by closed curves. In the more general cases, the concept of area becomes theoretically very difficult.
The area of a planar set is defined by reducing to the areas of simpler sets. The area cannot be "calculated", unless we first have a definition of "area" (although this is common practice in school mathematics).
Starting point
The area of a rectangle
The area of a rectangle is
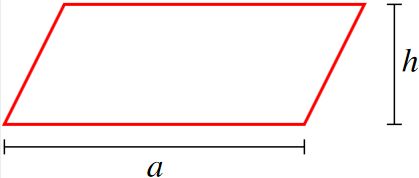
Definition: Area of a Parallelogram
The area of a parallelogram is
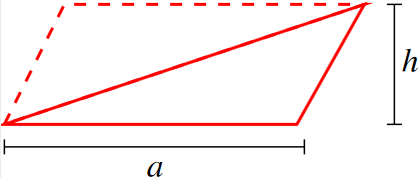
Definition: Area of a triangle
The area of a triangle is (by definition) \[ A=\frac{1}{2}ah. \]
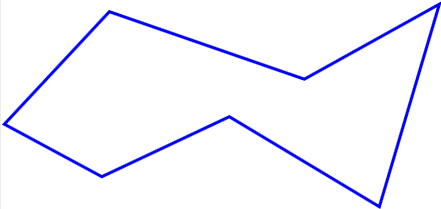
Polygon
A (simple) polygon is a plane set bounded by a closed curve that consists of a finite number of line segments without self-intersections.
Definition: Area of a polygon
The area of a polygon is defined by dividing it into a
finite number of triangles (called a
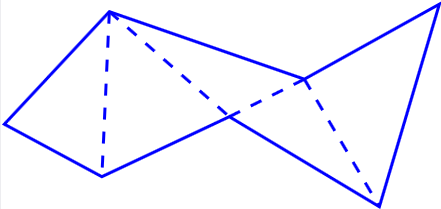
Theorem.
The sum of the areas of triangles in a triangulation of a polygon is the same for all triangulations.
General case
For a plane set \(\color{red} D\) bounded by a closed curve we can construct inner polygons \(\color{blue}P_i\) and outer polygons \(P_o\): \(\color{blue}P_i\color{black} \subset \color{red}D\color{black}\subset P_o\).
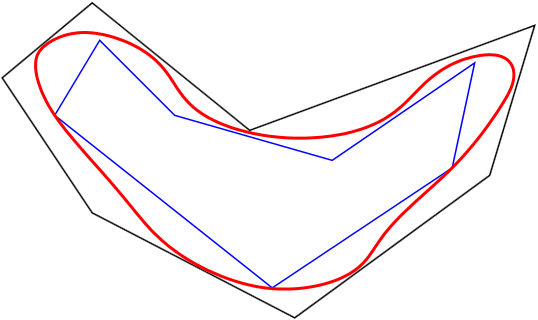
A surprise: The condition that \(D\) is bounded by a closed curve (without self-intersections) does not guarantee that it has an area! Reason: The boundary curve can be so "wiggly", that it has positive "area". The first such example was constucted by [W.F. Osgood, 1903]:
Wikipedia: Osgood curveExample
Derive the formula \(A=\pi R^2\) for a circle with radius \(R\) by choosing regular inscrided and circumscribed \(n\)-gons as inner and outer polygons, and let \(n\to\infty\).
The solution is a voluntary exercise, where you need the limit \[\lim_{x\to 0}\frac{\sin x}{x} = 1.\] Hint: Show that the inscribed and circumscribed areas are \[ \pi R^2\frac{\sin (2\pi/n)}{2\pi/n} \ \text{ and }\ \pi R^2\frac{\tan \pi/n}{\pi/n}.\]
