Differential and Integral Calculus
| Sivusto: | Aalto OpenLearning |
| Kurssi: | Differential and Integral Calculus 2021 |
| Kirja: | Differential and Integral Calculus |
| Tulostanut: | Гість-користувач |
| Tulostettu: | tiistaina 20. tammikuuta 2026, 02.40 |
1. Sequences
Basics of sequences
This section contains the most important definitions about sequences. Through these definitions the general notion of sequences will be explained, but then restricted to real number sequences.
Definition: Sequence
Let \(M\) be a non-empty set. A sequence is a function:
\[f:\mathbb{N}\rightarrow M.\]
Occasionally we speak about a sequence in \(M\).
Note. Characteristics of the set \(\mathbb{N}\) give certain characteristics to the sequence. Because \(\mathbb{N}\) is ordered, the terms of the sequence are ordered.
Definition: Terms and Indices
A sequence can be denoted denoted as
\((a_{1}, a_{2}, a_{3}, \ldots) = (a_{n})_{n\in\mathbb{N}} = (a_{n})_{n=1}^{\infty} = (a_{n})_{n}\)
instead of \(f(n).\) The numbers \(a_{1},a_{2},a_{3},\ldots\in M\) are called the terms of the sequence.
Because of the mapping \[\begin{aligned} f:\mathbb{N} \rightarrow & M \\ n \mapsto & a_{n}\end{aligned}\] we can assign a unique number \(n\in\mathbb{N}\) to each term. We write this number as a subscript and define it as the index; it follows that we can identify any term of the sequence by its index.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | \(\ldots\) |
|---|---|---|---|---|---|---|---|---|---|---|
| \(\downarrow\) | \(\downarrow\) | \(\downarrow\) | \(\downarrow\) | \(\downarrow\) | \(\downarrow\) | \(\downarrow\) | \(\downarrow\) | \(\downarrow\) | ||
| \(a_{n}\) | \(a_{1}\) | \(a_{2}\) | \(a_{3}\) | \(a_{4}\) | \(a_{5}\) | \(a_{6}\) | \(a_{7}\) | \(a_{8}\) | \(a_{9}\) | \(\ldots\) |
A few easy examples
Example 1: The sequence of natural numbers
The sequence \((a_{n})_{n}\) defined by \(a_{n}:=n,\,n\in \mathbb{N}\) is called the sequence of natural numbers. Its first few terms are: \[a_1=1,\, a_2=2,\, a_3=3, \ldots\] This special sequence has the property that every term is the same as its index.
![]()
Example 2: The sequence of triangular numbers
Triangular numbers get their name due to the following geometric visualization: Stacking coins to form a triangular shape gives the following diagram:

To the first coin in the first layer we add two coins in a second layer to form the second picture \(a_2\). In turn, adding three coins to \(a_2\) forms \(a_3\). From a mathematical point of view, this sequence is the result of summing natural numbers. To calculate the 10th triangular number we need to add the first 10 natural numbers: \[D_{10} = 1+2+3+\ldots+9+10\] In general form the sequence is defined as: \(D_{n} = 1+2+3+\ldots+(n-1)+n.\)

This motivates the following definition:
Notation and Definition: Sum sequence
Let \((a_n)_n, a_n: \mathbb{N}\to M\) be a sequence with terms \(a_n\), the sum is written: \[a_1 + a_2 + a_3 + \ldots + a_{n-1} + a_n =: \sum_{k=1}^n a_k\] The sign \(\sum\) is called sigma. Here, the index \(k\) increases from 1 to \(n\).
Sum sequences are sequences whose terms are formed by summation of previous terms.
Thus the nth triangular number can be written as: \[D_n = \sum_{k=1}^n k\]
Example 3: Sequence of square numbers
The sequence of square numbers \((q_n)_n\) is defined by: \(q_n=n^2\). The terms of this sequence can also be illustrated by the addition of coins.
Interestingly, the sum of two consecutive triangular numbers is a square number. So, for example, we have: \(3+1=4\) and \(6+3=9\). In general this gives the relationship:
\[q_n=D_n + D_{n-1}\]

Example 4: Sequence of cube numbers
Analogously to the sequence of square number, we give the definition of cube numbers as \[a_n := n^3.\] The first terms of the sequence are: \((1,8,27,64,125,\ldots)\).

Example 5.
Let \((q_n)_n\) with \(q_n := n^2\) be the sequence of square numbers \[\begin{aligned}(1,4,9,16,25,36,49,64,81,100 \ldots)\end{aligned}\] and define the function \(\varphi(n) = 2n\). The composition \((q_{2n})_n\) yields: \[\begin{aligned}(q_{2n})_n &= (q_2,q_4,q_6,q_8,q_{10},\ldots) \\ &= (4,16,36,64,100,\ldots).\end{aligned}\]
Definition: Sequence of differences
Given a sequence \((a_{n})_{n}=a_{1},\, a_{2},\, a_{3},\ldots,\, a_{n},\ldots\); then \[(a_{n+1}-a_{n})_{n}:=a_{2}-a_{1}, a_{3}-a_{2},\dots\] is called the 1st difference sequence of \((a_{n})_{n}\)
The 1st difference sequence of the 1st difference sequence is called the 2nd difference sequence. Analogously the \(n\)th difference< sequence is defined.
Example 6.
Given the sequence \((a_n)_n\) with \(a_n := \frac{n^2+n}{2}\), i.e. \[\begin{aligned}(a_n)_n &= (1,3,6,10,15,21,28,36,\ldots)\end{aligned}\] Let \((b_n)_n\) be its 1st difference sequence. Then it follows that \[\begin{aligned}(b_n)_n &= (a_2-a_1, a_3-a_2, a_4-a_3,\ldots) \\ &= (2,3,4,5,6,7,8,9)\end{aligned}\] A term of \((b_n)_n\) has the general form \[\begin{aligned}b_n &= a_{n+1}-a_{n} \\ &= \frac{(n+1)^2+(n+1)}{2} - \frac{n^2+n)}{2} \\ &= \frac{(n+1)^2+(n+1)-n^2 - n }{2} \\ &= \frac{(n^2+2n+1)+1-n^2}{2} \\ &= \frac{2n+2}{2} \\ &= n + 1.\end{aligned}\]
Some important sequences
There are a number of sequences that can be regarded as the basis of many ideas in mathematics, but also can be used in other areas (e.g. physics, biology, or financial calculations) to model real situations. We will consider three of these sequences: the arithmetic sequence, the geometric sequence, and Fibonacci sequence, i.e. the sequence of Fibonacci numbers.
The arithmetic sequence
There are many definitions of the arithmetic sequence:
Definition A: Arithmetic sequence
A sequence \((a_{n})_{n}\) is called the arithmetic sequence, when the difference \(d \in \mathbb{R}\) between two consecutive terms is constant, thus: \[a_{n+1}-a_{n}=d \text{ with } d=const.\]
Note: The explicit rule of formation follows directly from definition A: \[a_{n}=a_{1}+(n-1)\cdot d\] For the \(n\)th term of an arithmetic sequence we also have the recursive formation rule: \[a_{n+1}=a_n + d.\]
Definition B: Arithmetic sequence
A non-constant sequence \((a_{n})_{n}\) is called an arithmetic sequence (1st order) when its 1st difference sequence is a sequence of constant value.
This rule of formation gives the arithmetic sequence its name: The middle term of any three consecutive terms is the arithmetic mean of the other two, for example:
\[a_2 = \frac{a_1+a_3}{2}.\]
Example 1.
The sequence of natural numbers \[(a_n)_n = (1,2,3,4,5,6,7,8,9,\ldots)\] is an arithmetic sequence, because the difference, \(d\), between two consecutive terms is always given as \(d=1\).
The geometric sequence
The geometric sequence has multiple definitions:
Definition: Geometric sequence
A sequence \((a_{n})_{n}\) is called a geometric sequence when the ratio of any two consecutive terms is always constant \(q\in\mathbb{R}\), thus \[\frac{a_{n+1}}{a_{n}}=q \text{ for all } n\in\mathbb{N}.\]
Note.The recursive relationship \(a_{n+1} = q\cdot a_n \) of the terms of the geometric sequence and the explicit formula for the calculation of the n th term of a geometric sequence \[a_n=a_1\cdot q^{n-1}\] follows directly from the definition.
Again the name and the rule of formation of this sequence are connected: Here, the middle term of three consecutive terms is the geometric mean of the other two, e.g.: \[a_2 = \sqrt{a_1\cdot a_3}.\]
Example 2.
Let \(a\) and \(q\) be fixed positive numbers. The sequence \((a_n)_n\) with \(a_n := aq^{n-1}\), i.e. \[\left( a_1, a_2, a_3, a_4,\ldots \right) = \left( a, aq, aq^2, aq^3,\ldots \right)\] is a geometric sequence. If \(q\geq1\) the sequence is monotonically increasing. If \(q<1\) it is strictly decreasing. The corresponding range \({a,aq,aq^2, aq^3}\) is finite in the case \(q=1\) (namely, a singleton), otherwise it is infinite.
The Fibonacci sequence
The Fibonacci sequence is famous because it plays a role in many biological processes, for instance in plant growth, and is frequently found in nature. The recursive definition is:
Definition: Fibonacci sequence
Let \(a_0 = a_1 = 1\) and let \[a_n := a_{n-2}+a_{n-1}\] for \(n\geq2\). The sequence \((a_n)_n\) is then called the Fibonacci sequence. The terms of the sequence are called the Fibonacci numbers.
The sequence is named after the Italian mathematician Leonardo of Pisa (ca. 1200 AD), also known as Fibonacci (son of Bonacci). He considered the size of a rabbit population and discovered the number sequence: \[(1,1,2,3,5,8,13,21,34,55,\ldots),\]
Example 3.
The structure of sunflower heads can be described by a system of two spirals, which radiate out symmetrically but contra rotating from the centre; there are 55 spirals which run clockwise and 34 which run counter-clockwise.
Pineapples behave very similarly. There we have 21 spirals running in one direction and 34 running in the other. Cauliflower, cacti, and fir cones are also constructed in this manner.

Convergence, divergence and limits
The following chapter deals with the convergence of sequences. We will first introduce the idea of zero sequences. After that we will define the concept of general convergence.
Preliminary remark: Absolute value in \(\mathbb{R}\)
The absolute value function \(x \mapsto |x|\) is fundamental in the study of convergence of real number sequences. Therefore we should summarise again some of the main characteristics of the absolute value function:
Definition: Absolute Value
For any given number \(x\in\mathbb{R}\) its absolute value \(|x|\) is defined by \[\begin{aligned}|x|:=\begin{cases}x & \text{for }x\geq0,\\ -x & \text{for }x<0.\end{cases}\end{aligned}\]
Graph of the absolute value function
Theorem: Calculation Rule for the Absolute Value
For \(x,y\in\mathbb{R}\) the following is always true:
\(|x|\geq0,\)
\(|x|=0\) if and only if \(x=0.\)
\(|x\cdot y|=|x|\cdot|y|\) (Multiplicativity)
\(|x+y|\leq|x|+|y|\) (Triangle Inequality)
Parts 1.-3. Results follow directly from the definition and by dividing it up into separate cases of the different signs of \(x\) and \(y\)
Part 4. Here we divide the triangle inequality into different cases.
Case 1.
First let \(x,y \geq 0\). Then it follows that \[\begin{aligned}|x+y|=x+y=|x|+|y|\end{aligned}\] and the desired inequality is shown.
Case 2.Next let \(x,y < 0\). Then: \[\begin{aligned}|x+y|=-(x+y)=(-x)+ (-y)=|x|+|y|\end{aligned}\]
Case 3.Finally we consider the case \(x\geq 0\) and \(y<0\). Here we have two subcases:
For \(x \geq -y\) we have \(x+y\geq 0\) and thus \(|x+y|=x+y\) from the definition of absolute value. Because \(y<0\) then \(y<-y\) and therefore also \(x+y < x-y\). Overall we have: \[\begin{aligned}|x+y| = x+y < x-y = |x|+|y|\end{aligned}\]
For \(x < -y\) then \(x+y<0\). We have \(|x+y|=-(x+y)=-x-y\). Because \(x\geq0\), we have \(-x < x\) and thus \(-x-y\leq x-y\). Overall we have: \[\begin{aligned}|x+y| = -x-y \leq x-y = |x|+|y|\end{aligned}\]
The case \(x<0\) and \(y\geq0\) we prove it analogously to the case 3, in which \(x\) and \(y\) are exchanged.
\(\square\)
Zero sequences
Definition: Zero sequence
A sequence \((a_{n})_{n}\) s called a zero sequence, if for every \(\varepsilon>0,\) there exists an index \(n_{0}\in\mathbb{N}\) such that \[|a_{n}| < \varepsilon\] for every \(n\geq n_{0},\, n\in\mathbb{N}\). In this case we also say that the sequence converges to zero.
Informally: We have a zero sequence, if the terms of the sequence with high enough indices are arbitrarily close to zero.
Example 1.
The sequence \((a_n)_n\) defined by \(a_{n}:=\frac{1}{n}\), i.e. \[\left(a_{1},a_{2},a_{3},a_{4},\ldots\right):=\left(\frac{1}{1},\frac{1}{2},\frac{1}{3},\frac{1}{4},\ldots\right)\] is called the harmonic sequence. Clearly, it is positive for all \(n\in\mathbb{N}\), however as \(n\) increases the absolute value of each term decreases getting closer and closer to zero.
Take for example \(\varepsilon := \frac{1}{5000}\), then choosing the index \(n_0 = 5000\), it follows that \(a_n<\frac{1}{5000}=\varepsilon\), for all \(n\geq n_0\).
The harmonic sequence converges to zero
Example 2.
Consider the sequence \[(a_n)_n \text{ where } a_n:=\frac{1}{\sqrt{n}}.\] Let \(\varepsilon := \frac{1}{1000}\).We then obtain the index \(n_0=1000000\) in this manner that for all terms \(a_n\) where \(n\geq n_0\) \(a_n < \frac{1}{1000}=\varepsilon\).
Note. To check whether a sequence is a zero sequence, you must choose an (arbitrary) \(\varepsilon \in \mathbb{R}\) where \(\varepsilon > 0\). Then search for a index \(n_0\), after which all terms \(n\) are smaller then said \(\varepsilon\).
Example 3.
We consider the sequence \((a_n)_n\), defined by \[a_n := \left( -1 \right)^n \cdot \frac{1}{n^2}.\]
Because of the factors \((-1)^n\) two consecutive terms have different signs; we call a sequence whose signs change in this way an alternating sequence.
We want to show that this sequence is a zero sequence. According to the definition we have to show that for every \(\varepsilon > 0\) there exist \(n_0 \in \mathbb{N}\), such that we have the inequality: \[|a_n|< \varepsilon\] for every term \(a_n\) where \(n\geq n_0\).
Firstly we let \(\varepsilon > 0\) be an arbitrary constant. Because the inequality \( |a_n|< \varepsilon\) must hold true for an arbitrary \(\varepsilon\) we must find the index \(n_0\) which depends on each \(\varepsilon\). More exactly: The inequality \[|a_{n_0}|=\left| \frac{1}{{n_0}^2} \right|= \frac{1}{{n_0}^2}<\varepsilon\] must be true for the index \(n_0\). Solve for \(n_0\): \[n_0 > \frac{1}{\sqrt{\varepsilon}},\] this index \(n_0\) gives our desired characteristic for every \(\varepsilon\).
Negative examples
The following are examples of non-convergent alternating sequences:
\(a_n = (-1)^n\)
\(a_n = (-1)^n \cdot n\)
Theorem: Characteristics of Zero sequences
Let \((a_n)_n\) and \((b_n)_n\) be two sequences. Then:
Let \((a_n)_n\) be a zero sequence, if \(b_n = a_n\) or \(b_n = -a_n\) for all \(n\in\mathbb{N}\) then \((b_n)_n\) is also a zero sequence.
Let \((a_n)_n\) be a zero sequence, if \(-a_n\leq b_n \leq a_n\) for all \(n\in\mathbb{N}\) then \((b_n)_n\) is also a zero sequence.
Let \((a_n)_n\) be a zero sequence, then \((c\cdot a_n)_n\) where \(c \in \mathbb{R}\) is also a zero sequence.
If \((a_n)_n\) and \((b_n)_n\) are zero sequences, then \((a_n + b_n)_n\) is also a zero sequence.
Parts 1 and 2. If \((a_n)_n\) is a zero sequence, then according to the definition there is an index \(n_0 \in \mathbb{N}\), such that \(|a_n|<\varepsilon\) for every \(n\geq n_0\) and an arbitrary \(\varepsilon\in\mathbb{R}\). But then we have \(|b_n|\leq|a_n|<\varepsilon\); this proves parts 1 and 2 are correct.
Part 3. If \(c=0\), then the result is trivial. Let \(c\neq0\) and choose \(\varepsilon > 0\) such that \[\begin{aligned}|a_n|<\frac{\varepsilon}{|c|}\end{aligned}\] for all \(n\geq n_0\). Rearranging we get: \[\begin{aligned} |c|\cdot|a_n|=|c\cdot a_n|<\varepsilon\end{aligned}\]
Part 4.
Because \((a_n)_n\) is a zero sequence, by the definition we have \(|a_n|<\frac{\varepsilon}{2}\) for all \(n\geq n_0\). Analogously, for the zero sequence \((b_n)_n\) there is a \(m_0 \in \mathbb{N}\) with \(|b_n|<\frac{\varepsilon}{2}\) for all \(n\geq m_0\).
Then for all \(n > \max(n_0,m_0)\) it follows (using the triangle inequality) that: \[\begin{aligned}|a_n + b_n|\leq|a_n|+|b_n|<\frac{\varepsilon}{2}+\frac{\varepsilon}{2} = \varepsilon\end{aligned}\]
\(\square\)
Convergence, divergence
The concept of zero sequences can be expanded to give us the convergence of general sequences:
Definition: Convergence and Divergence
A sequence \((a_{n})_{n}\) is called convergent to \(a\in\mathbb{R}\), if for every \(\varepsilon>0\) there exists a \(n_{0}\) such that: \[|a_{n}-a| \lt \varepsilon \text{ for all }n\in\mathbb{N}_{0},\text{ where }n\geq n_{0}\]
An equivalent definition can be defined by:
A sequence \((a_{n})_{n}\) is called convergent to \(a\in\mathbb{R}\), if \((a_{n}-a)_{n}\) is a zero sequence.
Example 4.
We consider the sequence \((a_n)_n\) where \[a_n=\frac{2n^2+1}{n^2+1}.\] By plugging in large values of \(n\), we can see that for \(n\to\infty\) \(a_n \to 2\) and therefore we can postulate that the limit is \(a=2\).
For a vigorous proof, we show that for every \(\varepsilon > 0\) there exists an index \(n_0\in\mathbb{N}\), such that for every term \(a_n\) with \(n>n_0\) the following relationship holds: \[\left| \frac{2n^2+1}{n^2+1} - 2\right| < \varepsilon.\]
Firstly we estimate the inequality: \[\begin{aligned}\left|\frac{2n^2+1}{n^2+1}-2\right| =&\left|\frac{2n^2+1-2\cdot\left(n^2+1\right)}{n^2+1}\right| \\ =&\left|\frac{2n^2+1-2n^2-2}{n^2+1}\right| \\ =&\left|-\frac{1}{n^2+1}\right| \\ =&\left|\frac{1}{n^2+1}\right| \\ <&\frac{1}{n}.\end{aligned}\]
Now, let \(\varepsilon > 0\) be an arbitrary constant. We then choose the index \(n_0\in\mathbb{N}\), such that \[n_0 > \frac{1}{\varepsilon} \text{, or equivalently, } \frac{1}{n_0} < \varepsilon.\] Finally from the above inequality we have: \[\left|\frac{2n^2+1}{n^2+1}-2\right| < \frac{1}{n} < \frac{1}{n_0} < \varepsilon,\] Thus we have proven the claim and so by definition \(a=2\) is the limit of the sequence.
\(\square\)
If a sequence is convergent, then there is exactly one number which is the limit. This characteristic is called the uniqueness of convergence.
Theorem: Uniqueness of Convergence
Let \((a_{n})_{n}\) be a sequence that converges to \(a\in\mathbb{R}\) and to \(b\in\mathbb{R}\). This implies \(a=b\).
Assume \(a\ne b\); choose \(\varepsilon\in\mathbb{R}\) with \(\varepsilon:=\frac{1}{3}|a-b|.\) Then in particular \([a-\varepsilon,a+\varepsilon]\cap[b-\varepsilon,b+\varepsilon]=\emptyset.\)
Because \((a_{n})_{n}\) converges to \(a\), there is, according to the definition of convergence, a index \(n_{0}\in\mathbb{N}\) with \(|a_{n}-a|< \varepsilon\) for \(n\geq n_{0}.\) Furthermore, because \((a_{n})_{n}\) converges to \(b\) there is also a \(\widetilde{n_{0}}\in\mathbb{N}\) with \(|a_{n}-b|< \varepsilon\) for \(n\geq\widetilde{n_{0}}.\) For \(n\geq\max\{n_{0},\widetilde{n_{0}}\}\) we have:
\[\begin{aligned}\varepsilon\ = &\ \frac{1}{3}|a-b| \Rightarrow\\
3\varepsilon\ = &\ |a-b|\\
= &\ |(a-a_{n})+(a_{n}-b)|\\
\leq &\ |a_{n}-a|+|a_{b}-b|\\
< &\ \varepsilon+\varepsilon=2\varepsilon,\end{aligned}\]
Consequently we have obtained \(3\varepsilon\leq2\varepsilon\), which is a contradiction as \(\varepsilon>0\). Therefore the assumption must be wrong, so \(a=b\).
\(\square\)
Definition: Divergent, Limit
If provided that a sequence \((a_{n})_{n}\) and an \(a\in\mathbb{R}\) exist, to which the sequence converges, then the sequence is called convergent and \(a\) is called the limit of the sequence, otherwise it is called divergent.
Notation. \((a_{n})_{n}\) is convergent to \(a\) is also written: \[a_{n}\rightarrow a,\text{ or }\lim_{n\rightarrow\infty}a_{n}=a.\] Such notation is allowed, as the limit of a sequence is always unique by the above Theorem (provided it exists).
Theorem: Bounded Sequences
A convergent sequence \((a_n)_n\) is bounded i.e. there exists a constant \(r\in\mathbb{R}\) such that: \[|a_n| \lt r\] for all \(n\in\mathbb{N}\).
We assume that the sequence \((a_n)_n\) has the limit \(a\). By the definition of convergence, we have that \(|a_n - a|<\varepsilon\) for all \(\varepsilon \in \mathbb{R}\) and \(n\geq n_0\). Choosing \(\varepsilon = 1\) gives:
\[\begin{aligned}|a_n|-|a|&\ \leq |a_n -a| \\
&\ < 1,\end{aligned}\]
And therefore also \(|a_n|\leq |a|+1\).
Thus for all \(n\in \mathbb{N}\): \[|a_n|\leq \max \left\{ |a_1|,|a_2|,\ldots,|a_{n_0}|,|a|+1 \right\}=:r\]
\(\square\)
Rules for convergent sequences
Theorem: Subsequences
Let \((a_{n})_{n}\) be a sequence such that \(a_{n}\rightarrow a\) and let \((a_{\varphi(n)})_{n}\) be a subsequence of \((a_{n})_{n}\). Then it follows that \((a_{\varphi(n)})_{n}\rightarrow a\).
Informally: If a sequence is convergent then all of its subsequences are also convergent and in fact converge to the same limit as the original.
By the definition of a subsequence \(\varphi(n)\geq n\). Because \(a_{n}\rightarrow a\) it is implicated that \(|a_{n}-a|<\varepsilon\) for \(n\geq n_{0}\), therefore \(|a_{\varphi(n)}-a|<\varepsilon\) for these indices \(n\).
\(\square\)
Theorem: Rules
Let \((a_{n})_{n}\) and \((b_{n})_{n}\) be sequences with \(a_{n}\rightarrow a\) and \(b_{n}\rightarrow b\). Then for \(\lambda, \mu \in \mathbb{R}\) it follows that:
\(\lambda \cdot (a_n)+\mu \cdot (b_n) \to \lambda \cdot a + \mu \cdot b\)
\((a_n)\cdot (b_n) \to a\cdot b\)
Informally: Sums, differences and products of convergent sequences are convergent.
Part 1. Let \(\varepsilon > 0\). We must show, that for all \(n \geq n_0\) it follows that: \[|\lambda \cdot a_n + \mu \cdot b_n - \lambda \cdot a - \mu \cdot b| < \varepsilon.\] The left hand side we estimate using: \[|\lambda (a_n-a)+\mu (b_n - b)| \leq |\lambda|\cdot|a_n-a|+|\mu|\cdot|b_n-b|.\]
Because \((a_n)_n\) and \((b_n)_n\) converge, for each given \(\varepsilon > 0\) it holds true that: \[\begin{aligned}|a_n - a| <\ \varepsilon_1 := &\ \textstyle \frac{\varepsilon}{2|\lambda|} \text{ for all }n\geq n_0\\ |b_n - b| <\ \varepsilon_2 := &\ \textstyle \frac{\varepsilon}{2|\mu|} \text{ for all }n\geq n_1\end{aligned}\]
Therefore \[\begin{aligned}|\lambda|\cdot|a_n-a|+|\mu|\cdot|b_n-b| < &\ |\lambda|\varepsilon_1 + |\mu|\varepsilon_2 \\ = &\ \textstyle{ \frac{\varepsilon}{2} + \frac{\varepsilon}{2} } = \varepsilon\end{aligned}\] for all numbers \(n \geq \max \{n_0,n_1\}\). Therefore the sequence \[\left( \lambda \left( a_n - a \right) + \mu \left( b_n - b \right) \right)_n\] is a zero sequence and the desired inequality is shown.
Part 2. Let \(\varepsilon > 0\). We have to show, that for all \(n > n_0\) \[|a_n b_n - a b| < \varepsilon.\] Furthermore an estimation of the left hand side follows: \[\begin{aligned} |a_n b_n - a b| =&\ |a_n b_n - a b_n + a b_n - ab| \\ \leq &\ |b_n|\cdot|a_n-a| + |a|\cdot|b_n - b|.\end{aligned}\] We choose a number \(B\), such that \(|b_n| \lt b\) for all \(n\) and \(|a| \lt b\). Such a value of \(B\) exists by the Theorem of convergent sequences being bounded. We can then use the estimation: \[\begin{aligned}|b_n|\cdot|a_n-a| + |a|\cdot|b_n - b| <&\ B \cdot \left(|a_n - a| + |b_n - b| \right).\end{aligned}\] For all \(n>n_0\) we have \(|a_n - a|<\frac{\varepsilon}{2\cdot B}\) and \(|b_n - b|<\frac{\varepsilon}{2\cdot B}\), and - putting everything together - the desired inequality it shown.
\(\square\)
2. Series
Table of Content
Convergence
Convergence
If the sequence of partial sums \((s_n)\) has a limit \(s\in \mathbb{R}\), then the series of the sequence \((a_k)\) converges and its sum is \(s\). This is denoted by \[ a_1+a_2+\dots =\sum_{k=1}^{\infty} a_k = \lim_{n\to\infty}\underbrace{\sum_{k=1}^{n} a_k}_{=s_{n}} = s. \]
Indexing
The partial sums should be indexed in the same way as the sequence \((a_k)\); e.g. the partial sums of a sequence \((a_k)_{k=0}^{\infty}\) are \(s_0= a_0, s_1=a_0+a_1\) etc.
The indexing of a series can be shifted without altering the series: \[\sum_{k=1}^{\infty} a_k =\sum_{k=0}^{\infty} a_{k+1} = \sum_{k=2}^{\infty} a_{k-1}.\]
In a concrete way: \[\sum_{k=1}^{\infty} \frac{1}{k^2}=1+\frac{1}{4}+\frac{1}{9}+\dots= \sum_{k=0}^{\infty} \frac{1}{(k+1)^2}\]
Interactivity.
Compute partial sums of the series \(\displaystyle\sum_{k=0}^{\infty}a_{k}\)
\(k\)th-element of the series: , start summation at
Divergence of a series
A series that does ot converge is divergent. This can happen in three different ways:
- the partial sums tend to infinity
- the partial sums tend to minus infinity
- the sequence of partial sums oscillates so that there is no limit.
In the case of a divergent series the symbol \(\displaystyle\sum_{k=1}^{\infty} a_k\) does not really mean anything (it isn't a number). We can then interpret it as the sequence of partial sums, which is always well-defined.
Basic results
Geometric series
A geometric series \[\sum_{k=0}^{\infty} aq^k\] converges if \(|q|<1\) (or \(a=0\)), and then its sum is \(\frac{a}{1-q}\). If \(|q|\ge 1\), then the series diverges.
Proof. The partial sums satisfy
\[\sum_{k=0}^{n} aq^k =\frac{a(1-q^{n+1})}{1-q},\]
from which the claim follows.
\(\square\)
More generally \[\sum_{k=i}^{\infty} aq^k = \frac{aq^i}{1-q} = \frac{\text{1st term of the series}}{1-q},\text{ for } |q|<1.\]
Example 1.
Calculate the sum of the series \[\sum_{k=1}^{\infty}\frac{3}{4^{k+1}}.\]
Solution. Since \[\frac{3}{4^{k+1}} = \frac{3}{4}\cdot \left( \frac{1}{4}\right)^k,\] this is a geometric series. The sum is \[\frac{3}{4}\cdot \frac{1/4}{1-1/4} = \frac{1}{4}.\]
Rules of summation
Properties of convergent series:
- \(\displaystyle{\sum_{k=1}^{\infty} (a_k+b_k) = \sum_{k=1}^{\infty} a_k + \sum_{k=1}^{\infty} b_k}\)
- \(\displaystyle{\sum_{k=1}^{\infty} (c\, a_k) = c\sum_{k=1}^{\infty} a_k}\), where \(c\in \mathbb{R}\) is a constant
Proof. These follow from the corresponding properties for limits of a sequence.
\(\square\)
Note: Compared to limits, there is no similar product-rule for series, because even for sums of two elements we have \[(a_1+a_2)(b_1+b_2) \neq a_1b_1 +a_2b_2.\] The correct generalization is the Cauchy product of two series, where also the cross terms are taken into account.
Theorem 1.
If the series \(\displaystyle{\sum_{k=1}^{\infty} a_k}\) converges, then \[\displaystyle{\lim_{k\to \infty} a_k =0}.\]
Conversely: If \[\displaystyle{\lim_{k\to \infty} a_k \neq 0},\] then the series \(\displaystyle{\sum_{k=1}^{\infty} a_k}\) diverges.
If the sum of the series is \(s\), then \(a_k=s_k-s_{k-1}\to s-s=0\).
\(\square\)
Note: The property \(\lim_{k\to \infty} a_k = 0\) cannot be used to justify the convergence of a series; cf. the following examples. This is one of the most common elementary mistakes many people do when studying series!
Example
Explore the convergence of the series \[\sum_{k=1}^{\infty} \frac{k}{k+1} = \frac{1}{2}+\frac{2}{3}+\frac{3}{4}+\dots\]
Solution. The limit of the general term of the series is \[\lim_{k\to\infty}\frac{k}{k+1} = 1.\] As this is different from zero, the series diverges.
Harmonic series
The harmonic series \[\sum_{k=1}^{\infty} \frac{1}{k} = 1+\frac{1}{2}+\frac{1}{3}+\dots\] diverges, although the limit of the general term \(a_k=1/k\) equals zero.
This is a classical result first proven in the 14th century by Nicole Oresme after which a number of proofs using different approaches have been published. Here we present two different approaches for comparison.
i) An elementary proof by contradiction. Suppose, for the sake of contradiction, that the harmonic series converges i.e. there exists \(s\in\mathbb{R}\)
such that \(s = \sum_{k=1}^{\infty}1/k\). In this case
\[
s = \left(\color{#4334eb}{1} + \color{#eb7134}{\frac{1}{2}}\right) + \left(\color{#4334eb}{\frac{1}{3}} +
\color{#eb7134}{\frac{1}{4}}\right) + \left(\color{#4334eb}{\frac{1}{5}} + \color{#eb7134}{\frac{1}{6}}\right) + \dots
= \sum_{k=1}^{\infty}\left(\color{#4334eb}{\frac{1}{2k-1}} + \color{#eb7134}{\frac{1}{2k}}\right).
\]
Now, by direct comparison we get
\[
\color{#4334eb}{\frac{1}{2k-1}} > \color{#eb7134}{\frac{1}{2k}} > 0, \text{ for all }k\ge 1~\Rightarrow~\sum_{k=1}^{\infty}\color{#4334eb}{\frac{1}{2k-1}} > \sum_{k=1}^{\infty}\color{#eb7134}{\frac{1}{2k}} = \frac{s}{2}
\]
hence following from the Properties of summation it follows that
\[
s = \sum_{k=1}^{\infty}\color{#4334eb}{\frac{1}{2k-1}} + \sum_{k=1}^{\infty}\color{#eb7134}{\frac{1}{2k}} = \sum_{k=1}^{\infty}\color{#4334eb}{\frac{1}{2k-1}} + \frac{1}{2}\underbrace{\sum_{k=1}^{\infty}\frac{1}{k}}_{=s}.
\]
\[
= \sum_{k=1}^{\infty}\color{#4334eb}{\frac{1}{2k-1}} + \frac{s}{2} > \sum_{k=1}^{\infty}\color{#eb7134}{\frac{1}{2k}} + \frac{s}{2} = \frac{s}{2} + \frac{s}{2} = s.
\]
But this implies that \(s>s\), a contradiction. Therefore, the initial assumption that the harmonic series converges must be false and thus the series diverges.
\(\square\)
ii) Proof using integral: Below a histogram with heights \(1/k\) lies the graph of
the function \(f(x)=1/(x+1)\), so comparing areas we have
\[\sum_{k=1}^{n} \frac{1}{k} \ge \int_0^n\frac{dx}{x+1} =\ln(n+1)\to\infty, \]
as \(n\to\infty\).
\(\square\)
Positive series
Summing a series is often difficult or even impossible in closed form, sometimes only a numerical approximation can be calculated. The first goal then is to find out whether a series is convergent or divergent.
A series \(\displaystyle{\sum_{k=1}^{\infty} p_k}\) is positive, if \(p_k > 0\) for all \(k\).
Convergence of positive series is quite straightforward:
Theorem 2.
A positive series converges if and only if the sequence of partial sums is bounded from above.
Why? Because the partial sums form an increasing sequence.
Example
Show that the partial sums of a superharmonic series \[\sum_{k=1}^{\infty}\frac{1}{k^2}\] satisfy \(s_n<2\) for all \(n\), so the series converges.
Solution. This is based on the formula \[\frac{1}{k^2} < \frac{1}{k(k-1)} = \frac{1}{k-1}-\frac{1}{k},\] for \(k\ge 2\), as it implies that \[\sum_{k=1}^n\frac{1}{k^2} < 1+ \sum_{k=2}^n\frac{1}{k(k-1)} =2-\frac{1}{n}< 2\] for all \(n\ge 2\).
This can also be proven with integrals.
Leonhard Euler found out in 1735 that the sum is actually \(\pi^2/6\). His proof was based on comparison of the series and product expansion of the sine function.
Absolute convergence
Definition
A series \(\displaystyle{\sum_{k=1}^{\infty} a_k}\) converges absolutely if the positive series \(\sum_{k=1}^{\infty} |a_k|\) converges.
Theorem 3.
An absolutely convergent series converges (in the usual sense) and \[\left| \sum_{k=1}^{\infty} a_k \right| \le \sum_{k=1}^{\infty} |a_k|.\]
This is a special case of the Comparison principle, see later.
Suppose that \(\sum_k |a_k|\) converges. We study separately the positive and negative
parts of \(\sum_k a_k\):
Let \[b_k=\max (a_k,0)\ge 0 \text{ and } c_k=-\min (a_k,0)\ge 0.\]
Since \(b_k,c_k\le |a_k|\), the positive series \(\sum b_k\) and \(\sum c_k\) converge by Theorem 2.
Also, \(a_k=b_k-c_k\), so \(\sum a_k\) converges as a difference of two convergent series.
\(\square\)
Example
Study the convergence of the alternating (= the signs alternate) series \[\sum_{k=1}^{\infty}\frac{(-1)^{k+1}}{k^2}=1-\frac{1}{4}+\frac{1}{9}-\dots\]
Solution. Since \[\displaystyle{\left| \frac{(-1)^{k+1}}{k^2}\right| =\frac{1}{k^2}}\] and the superharmonic series \[\sum_{k=1}^{\infty}\frac{1}{k^2}\] converges, then the original series is absolutely convergent. Therefore it also converges in the usual sense.
Alternating harmonic series
The usual convergence and absolute convergence are, however, different concepts:
Example
The alternating harmonic series \[\sum_{k=1}^{\infty}\frac{(-1)^{k+1}}{k} = 1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\dots\] converges, but not absolutely.
(Idea) Draw a graph of the partial sums \((s_n)\) to get the idea that even and odd index partial sums \(s_{2n}\) and \(s_{2n+1}\) are monotone and converge to the same limit.
The sum of this series is \(\ln 2\), which can be derived by integrating the formula of a geometric series.
points are joined by line segments for visualization purposes
Convergence tests
Comparison test
The preceeding results generalize to the following:
Theorem 4.
(Majorant) If \(|a_k|\le p_k\) for all \(k\) and
\(\sum_{k=1}^{\infty} p_k\) converges,
then also \(\sum_{k=1}^{\infty} a_k\) converges.
(Minorant) If \(0\le p_k \le a_k\) for all \(k\) and \(\sum p_k\) diverges, then also \(\sum a_k\) diverges.
Proof for Majorant. Since \[a_k=|a_k|-(|a_k|-a_k)\] and
\[0\le |a_k|-a_k \le 2|a_k|,\]
then \(\sum a_k\) is convergent as a difference of two convergent positive series.
Here we use the elementary convergence property (Theorem 2.) for positive series;
this is not a circular reasoning!
Proof for Minorant. It follows from the assumptions that the partial sums of \(\sum a_k\)
tend to infinity, and the series is divergent.
\(\square\)
Example
Study the convergence of \[ \sum_{k=1}^{\infty} \frac{1}{1+k^3} \ \text{ ja }\ \sum_{k=1}^{\infty} \frac{1}{\sqrt{k}}. \]
Solution. Since \[0<\frac{1}{1+k^3} < \frac{1}{k^3}\le \frac{1}{k^2}\] for all \(k\in \mathbb{N}\), the first series is convergent by the majorant principle.
On the other hand, \[\displaystyle{\frac{1}{\sqrt{k}}\ge \frac{1}{k}}\] for all \(k\in\mathbb{N}\), so the second series has a divergent harmonic series as a minorant. The latter series is thus divergent.
Ratio test
In practice, one of the best ways to study convergence/divergence of a series is the so-called ratio test, where the terms of the sequence are compared to a suitable geometric series:
Theorem 5a.
Suppose that there is a constant \(0< Q < 1\) so that \[ \left| \frac{a_{k+1}}{a_k} \right| \le Q\] starting from some index \(k\ge k_0\).
Then the series \(\sum a_k\) converges (and the rate of convergence is comparable to the geometric series \(\sum Q^k\), or is even higher).
We may assume that the inequality is valid for all indices \(k\), because the initial part has no effect on the convergence (although it has an effect to the sum!).
This now implies that
\[|a_{k}|\le Q|a_{k-1}|\le Q^2|a_{k-2}|\le \dots\le Q^k|a_0|,\]
so the series has a convergent geometric majorant.
\(\square\)
Limit form of ratio test
Theorem 5b.
Suppose that the limit \[\lim_{k\to \infty} \left| \frac{a_{k+1}}{a_k} \right| = q\] exists. Then the series \(\sum a_k\) \[ \begin{cases}\text{converges} & \text{ if } 0\le q< 1,\\ \text{diverges} & \text{ if } q > 1,\\ \text{nay be convergent or divergent} & \text{ if } q=1. \end{cases} \]
(Idea) For a geometric series the ratio of two consecutive terms is exactly \(q\). According to the ratio test, the convergence of some other series can also be investigated in a similar way, when the exact ratio \(q\) is replaced by the above limit.
In the formal definition of a limit \(\varepsilon =(1-q)/2>0\). Thus starting from some index \(k\ge k_{\varepsilon}\) we have \[ |a_{k+1}/a_k| < q + \varepsilon = (q+1)/2 = Q < 1, \] and the claim follows from Theorem 4.
In the case \(q>1\) the general term of the series does not go to zero, so the series diverges.
The last case \(q=1\) does not give any information.
This case occurs for the harmonic series (\(a_k=1/k\), divergent!) and superharmonic
(\(a_k=1/k^2\), convergent!) series. In these cases the convergence or divergence
must be settled in some other way, as we did before.
\(\square\)
Example
Is the series \[\sum_{k=1}^{\infty}\frac{(-1)^{k+1}k}{2^k}= \frac{1}{2}-\frac{2}{4}+\frac{3}{8}-\dots\] convergent?
Solution. Here \(a_k=(-1)^{k+1}k/2^k\), so \[ \left| \frac{a_{k+1}}{a_k}\right| = \left| \frac{(-1)^{k+2}(k+1)/2^{k+1}}{(-1)^{k+1}k/2^k}\right| =\frac{k+1}{2k} =\frac{1}{2}+\frac{1}{2k}\to \frac{1}{2} < 1, \] when \(k\to\infty\). By the ratio test the series is convergent.
3. Continuity
Table of Content
In this section we define a limit of a function \(f\colon S\to \mathbb{R}\) at a point \(x_0\). It is assumed that the reader is already familiar with limit of a sequence, the real line and the general concept of a function of one real variable.
Limit of a function
For a subset of real numbers, denoted by \(S\), assume that \(x_0\) is such point that there is a sequence of points \((x_k)\in S\) such that \(x_k\to x_0\) as \(k\to \infty\). Here the set \(S\) is often the set of all real numbers, but sometimes an interval (open or closed).
Example 1.
Note that it is not necessary for \(x_0\) to be in \(S\). For example, the sequence \(x_k = 1/k\to 0\) as \(k\to \infty\) in \(S=]0,2[\), and \(x_k\in S\) for all \(k=1,2,\ldots\) but \(0\) is not in \(S\).
Limit of a function
We consider a function \(f\) defined in the set \(S\). Then we define the limit of the function \(f\colon S\to \mathbb{R}\) at \(x_0\) as follows.
Definition 1: Limit of a function
Suppose that \(S\subset \mathbb{R}\) and \(f\colon S\to \mathbb{R}\) is a function. Then we say that \(f\) has a limit \(y_{0}\) at \(x_{0}\), and write \[\lim_{x \to x_{0}}f(x)=y_{0},\] if, \(f(x_{k})\to y_{0}\) as \(k\to \infty\) for every sequence \((x_{k})\) in \(S\setminus\{x_0\}\), such that \(x_{k}\to x_{0}\) as \(k\to \infty\).
Example 2.
The function \(f\colon \mathbb{R} \to \mathbb{R}\) defined by \(f(x)=x^2\) has a limit \(0\) at the point \(x=0\).
Function \(y=x^2\).
Example 3.
The function \(g\colon\mathbb{R}\to \mathbb{R}\) defined by \[g(x)= \left\{\begin{array}{rl}0 & \text{ for }x<0, \\ 1 & \text{ for }x\ge 0.\end{array}\right.\] does not have a limit at the point \(x=0\). To formally prove this, take sequences \((x_k)\), \((y_k)\) defined by \(x_k=1/k\) and \(y_k=-1/k\) for \(k=1,2,\ldots\). Then the both sequences are in \(S=\mathbb{R}\), but \(f(x_k)=1\) and \(f(y_k)=0\) for any \(k\).
Function \[g(x)= \left\{\begin{array}{rl}0 & \text{ for }x<0, \\ 1 & \text{ for }x\ge 0.\end{array}\right.\]
Example 4.
The function \(f(x)=x \sin(1/x)\), \(x>0\) does have the limit \(0\) at \(0\).
Function \(y=x\sin(1/x)\) for \(x>0\).
Example 5.
The function \(g(x)= \sin(1/x)\), \(x>0\) does not have a limit at \(0\).
Function \(y=\sin(1/x)\) for \(x>0\).
One-sided limits
An important property of limits is that they are always unique. That is, if \(\lim_{x\to x_0} f(x)=a\) and \(\lim_{x\to x_0} f(x)=b\), then \(a=b\). Although a function may have only one limit at a given point, it is sometimes useful to study the behavior of the function when \(x_k\) approaches the point \(x_0\) from the left or the right side. These limits are called the left and the right limit of the function \(f\) at \(x_0\), respectively.
Definition 2: One-sided limits
Suppose \(S\) is a set in \(\mathbb{R}\) and \(f\) is a function defined on the set \(S\setminus\{x_0\}\). Then we say that \(f\) has a left limit \(y_{0}\) at \(x_{0}\), and write \[\lim_{x \to x_{0}-}f(x)=y_{0},\] if, \(f(x_{k})\to y_{0}\) as \(k\to \infty\) for every sequence \((x_{k})\) in the set \(S\cap ]-\infty,x_0[ =\{ x\in S : x < x_0 \}\), such that \(x_{k}\to x_{0}\) as \(k\to \infty\).
Similarly, we say that \(f\) has a right limit \(y_{0}\) at \(x_{0}\), and write \[\lim_{x \to x_{0}+}f(x)=y_{0},\] if, \(f(x_{k})\to y_{0}\) as \(k\to \infty\) for every sequence \((x_{k})\) in the set \(S\cap ]x_0,\infty[ =\{ x\in S : x_0 < x \}\), such that \(x_{k}\to x_{0}\) as \(k\to \infty\).
Theorem 1: Limit of a function
A function \(f\colon S\to \mathbb{R}\) has a limit \(y_0\) at the point \(x_0\) if and only if \[\lim_{x \to x_{0}-}f(x)= \lim_{x \to x_{0}+}f(x)=y_{0}.\]
Example 6.
The sign function \[\mathrm{sgn}(x)= \frac{x}{|x|}\] is defined on \(S= \mathbb{R}\setminus 0\). Its left and right limits at \(0\) are \[\lim_{x\to 0-} \mathrm{sgn}(x)= -1,\qquad \lim_{x\to 0+} \mathrm{sgn}(x)= 1.\] However, the function \(\mathrm{sgn}(x)\) does not have a limit at \(0\).
Function \(y = \frac{x}{|x|}\).
Example 7.
Function \(f: \mathbb{R}\setminus 0 \to \mathbb{R}\) \[f(x) = \frac{1}{x}\] does not have one-sided limits at 0.
Limit rules
The following limit rules are immediately obtained from the definition and basic algebra of real numbers.
Theorem 2: Limit rules
Let \(c\in \mathbb{R}, \lim_{x\to x_{0}} f(x)=a\) and \(\lim_{x\to x_{0}} g(x)=b.\) Then
- \(\lim_{x\to x_{0}} (cf)(x)=ca\),
- \(\lim_{x\to x_{0}} (f+g)(x)=a+b\),
- \(\lim_{x\to x_{0}} (fg)(x)=ab\),
- \(\lim_{x\to x_{0}} (f/g)(x)=a/b \ (\text{if} \ b \neq 0)\).
Example 8.
Finding limits by calculating \(f(x_0)\):
a) \[\lim_{x\to 2}(5x-3)=10-3=7.\]
b) \[\lim_{x\to -2}\frac{3x+2}{x+5} = \frac{-6+2}{-2+5}=-\frac{4}{3}.\]
c) \[\lim_{x\to 2} \frac{x^2-4}{x-2} = \lim_{x\to 2} \frac{(x+2)(x-2)}{x-2} = \lim_{x\to 2}(x+2) = 4.\]
Limits and continuity
In this section, we define continuity of the function. The intutive idea behind continuity is that the graph of a continuous function is a connected curve. However, this is not sufficient as a mathematical definition for several reasons. For example, by using this definition, one cannot easily decide if \(\tan(x)\) is a continuous function or not.
For continuity of a function \(f\) at a given point \(x_0\), it is required that:
\(f(x_0)\) is defined,
\(\lim_{x \to x_0} f(x)\) exists (and is finite),
\(\lim_{x \to x_0} f(x) = f(x_0)\).
In other words:
Definition 2: Continuity
A function \(f\colon S\to \mathbb{R}\) is continuous at a point \(x_{0}\in S\), if \[\lim_{x\to x_{0}}f(x)=f(x_{0}).\] A function \(f\colon S\to \mathbb{R}\) is continuous, if it is continuous at every point \(x_{0}\in S\).
Example 1.
Let \(c\in \mathbb{R}\). Functions \(f,g,h\) defined by \(f(x)=c\), \(g(x)=x\), \(h(x)=|x|\) are continuous at every point \(x\in \mathbb{R}\).
Why? If \(x_{k}\to x_{0}\), then \(f(x_{k})=c\) and \(\lim_{k\to \infty}f(x_k)= c=f(x_{0})\). For \(g\), we have \(g(x_{k})=x_{k}\) and hence, \(\lim_{k\to\infty} g(x_k)=x_{0}=g(x_{0})\). Similarly, \(h(x_{k})=|x_{k}|\) and \(\lim_{k\to\infty}h(x_k)= |x_{0}|=h(x_{0})\).
Continuous functions \(y=c\), \(y=x\) and \(y=|x|\).
Example 2.
Let \(x_{0}\in \mathbb{R}\). We define a function \(f\colon\mathbb{R}\to \mathbb{R}\) by \[f(x)= \left\{\begin{array}{rl}2 & \text{ for }x \lt x_{0}, \\ 3 & \text{ for }x\geq x_{0}.\end{array}\right.\] Then \[\lim_{x \to x_{0}^{-}}f(x)=2,\text{ and } \lim_{x \to x_{0}^{+}}f(x)=3.\] Therefore \(f\) is not continuous at the point \(x_{0}\).
Some basic properties of continuous functions of one real variable are given next. From the limit rules (Theorem 2) we obtain:
Theorem 3.
The sum, the product and the difference of continuous functions are continuous. Then, in particular, polynomials are continuous functions. If \(f\) and \(g\) are polynomials and \(g(x_{0})\neq 0\), then \(f/g\) is continuous at a point \(x_{0}\).
A composition of continuous functions is continuous if it is defined:
Theorem 4.
Let \(f\colon \mathbb{R}\to\mathbb{R}\) and \(g\colon \mathbb{R}\to \mathbb{R}\). Suppose that \(f\) is continuous at a point \(x_{0}\) and \(g\) is continuous at \(f(x_{0})\). Then \(g\circ f\colon \mathbb{R}\to \mathbb{R}\) is continuous at a point \(x_{0}\).
Note. If \(f\) is continuous, then \(|f|\) is continuous.
Why?
Write \(g(x):=|x|\). Then \((g\circ f)(x)=|f(x)|\).
Note. If \(f\) and \(g\) are continuous, then \(\max (f,g)\) and \(\min (f,g)\) are continuous. (Here \(\max (f,g)(x):=\max \{f(x),g(x)\}\).)
Why?
Write \[\begin{cases}(a+b)+|a-b|=2\max(a,b), \\ (a+b)-|a-b|=2\min(a,b). \end{cases} \]
\[\text{Function }f(x)= \left\{\begin{array}{rl}2 & \text{ for }x\lt x_{0}, \\ 3 & \text{ for }x\geq x_{0}. \end{array}\right.\]
Delta-epsilon definition
The so-called \((\varepsilon,\delta)\)-definition for continuity is given next. The basic idea behind this test is that, for a function \(f\) continuous at \(x_0\), the values of \(f(x)\) should get closer to \(f(x_0)\) as \(x\) gets closer to \(x_0\).
This is the standard definition of continuity in mathematics, because it also works for more general classes of functions than ones on this course, but it not used in high-school mathematics. This important definition will be studied in-depth in Analysis 1 / Mathematics 1.
\((\varepsilon,\delta)\)-test:
Theorem 5: \((\varepsilon,\delta)\)-definition
Let \(f: S\to \mathbb{R}\). Then the following conditions are equivalent:
- \(\lim_{x\to x_0} f(x)= y_0\),
- For all \(\varepsilon> 0\) there exists \(\delta >0\) such that if \(0 < |x-x_0| < \delta\), then \(|f(x) - y_0| <\varepsilon\) for all \(x\in S\).
Example 3.
From Theorem 3 we already know that the function \(f: \mathbb{R} \to \mathbb{R}\) defined by \(f(x) = 4x\) is continuous. We can also use the \((\varepsilon,\delta)\)-definition to prove this.
Proof. Let \(x_0 \in \mathbb{R}\) and \(\varepsilon > 0\). Now \[|f(x) - f(x_0)| = |4x - 4x_0| = 4|x - x_0| < \varepsilon,\] when \[|x - x_0| < \delta \text{, where } \delta = \frac{\varepsilon}{4}.\]
So for all \(\varepsilon > 0\) there exists \(\delta > 0\) such that if \(|x - x_0| < \delta\), then \(|f(x) - f(x_0)| < \varepsilon\) for all \(x \in \mathbb{R}\). Thus by
Theorem 5 \(\lim_{x \to x_0} f(x) = f(x_0)\) for all \(x_0 \in \mathbb{R}\) and by definition this means that the function \(f: \mathbb{R} \to \mathbb{R}\) is continuous.
\(\square\)
Interactivity. \((\varepsilon, \delta)\) in example 3.
Example 4.
Let \(x_{0}\in \mathbb{R}\). We define a function \(f\colon\mathbb{R}\to \mathbb{R}\) by \[f(x)= \left\{\begin{array}{rl}2 & \text{ for }x \lt x_{0}, \\ 3 & \text{ for }x \geq x_{0}.\end{array}\right.\] In Example 2 we saw that this function is not continuous at the point \(x_0\). To prove this using the \((\varepsilon,\delta)\)-test, we need to find some \(\varepsilon > 0\) and some \(x_\delta \in \mathbb{R}\) such that for all \(\delta > 0\), \(|x_\delta - x_0| < \delta\), but \(|f(x_\delta) - f(x_0)| > \varepsilon\).
Proof. Let \(\delta > 0\) and \(\varepsilon = 1/2\). By choosing \(x_\delta = x_0 - \delta /2\), we have
\[0 < |x_\delta-x_0| = |x_0 - \frac{\delta}{2} + x_0| = \frac{\delta}{2} < \delta,\]
and
\[|f(x_\delta) - f(x_0)| = |2 - 3| = 1 > \varepsilon.\]
Therefore by Theorem 5 \(f\) is not continuous at the point \(x_{0}\).
\(\square\)
Interactivity. \((\varepsilon, \delta)\) in example 4.
Properties of continuous functions
This section contains some fundamental properties of continuous functions. We start with the Intermediate Value Theorem for continuous functions, also known as Bolzano's Theorem. This theorem states that a function that is continuous on a given (closed) real interval, attains all values between its values at endpoints of the interval. Intuitively, this follows from the fact that the graph of a function defined on a real interval is a continuous curve.
Theorem 6: Intermediate Value Theorem
If \(f\colon [a,b]\to \mathbb{R}\) is continuous and \(f(a) \lt s \lt f(b)\), then there is at least one \(c\in ]a,b[\) such that \(f(c)=s\).
The Intermediate Value Theorem.
Example 1.
Let function \(f:\mathbb{R} \to \mathbb{R}\), where \[f(x) = x^5 - 3x - 1.\] Show that there is at least one \(c \in \mathbb{R}\) such that \(f(c) = 0\).
Solution. As a polynomial function, \(f\) is continuous. And because \[f(1) = 1^5 - 3 \cdot 1 - 1 = -3 < 0\] and \[f(-1) = (-1)^5 - 3 \cdot (-1) - 1 = 1 > 0,\] by the Intermediate Value Theorem there is at least one \(c \in ]-1, 1[\) such that \(f(c) = 0\).
Function \(f(x) = x^5 - 3x - 1\).
Example 2.
Let \(f(x)=x^3-x=x(x^2-1)=x(x-1)(x-1)\).
By the Intermediate Value Theorem we have \(f(x)<0\) for \(x<-1\) or \(0 \lt x \lt 1\). Similarly, \(f(x)>0\) for \(-1 \lt x \lt 0\) or \(1 \lt x\), because:
- \(f(x)=0\) if and only if \(x=0\) or \(x=\pm 1\), and
- \(f(-2)<0, f(-1/2)>0, f(1/2)<0\) and \(f(2)>0\).
Function \(f(x) = x^3 - x\).
Next we prove that a continuous function defined on a closed real interval is necessarily bounded. For this result, it is important that the interval is closed. A counter example for an open interval is given after the next theorem.
Theorem 7.
Let \(f\colon [a,b]\to \mathbb{R}\) be continuous. Then \(f\) is bounded.
Note. If \(f\colon ]a,b[\to \mathbb{R}\) is continuous, it can be unbounded.
Example 4.
Let \(f\colon ]0,1]\to \mathbb{R}\), where \(f(x)=1/x\). Now \[\lim_{x\to 0+}f(x)=\infty.\]
Theorem 8.
Let \(f\colon [a,b]\to \mathbb{R}\) be continuous. Then there exist points \(c,d\in [a,b]\) such that \(f(c)\leq f(x)\leq f(d)\) for all \(x\in [a,b]\), i.e. \(f(c)\) is minimum and \(f(d)\) is maximum of \(f\) on the interval \([a,b]\).
Function \(f(x) = 1/x\) for \(x > 0\).
Example 5.
Let \(f:[-1,2] \to \mathbb{R}\), where \[f(x) = -x^3 - x + 3.\] The domain of the function is \([-1,2]\). To determine the range of the function, we first notice that the function is decreasing. We will now show this.
Let \(x_1 < x_2\). Then \[x_{1}^3 < x_{2}^3\] and \[-x_{1}^3 > -x_{2}^3.\]
Because \(x_1 < x_2\), \[-x_1^3-x_1 > -x_2^3 -x_2\] and \[-x_1^3-x_1 +3 > -x_2^3 -x_2 +3.\] Thus, if \(x_1 < x_2\) then \(f(x_1) > f(x_2)\), which means that the function \(f\) is decreasing.
We know that a decreasing function has its minimum value in the right endpoint of the interval. Thus, the minimum value of \(f:[-1,2] \to \mathbb{R}\) is \[f(2) = -2^3 - 2 + 3 = -7.\] Respectively, a decreasing function has it's maximum value in the left endpoint of the interval and so the maximum value of \(f:[-1,2] \to \mathbb{R}\) is \[f(-1) = -(-1)^3 - (-1) + 3 = 5.\]
As a polynomial function, \(f\) is continuous and it therefore has all the values between it's minimum and maximum values. Hence, the range of \(f\) is \([-7, 5]\).
Function \(-x^3 - x + 3\) for \([-1, 2]\).
Example 6.
Suppose that \(f\) is a polynomial. Then \(f\) is continuous on \(\mathbb{R}\) and, by Theorem 7, \(f\) is bounded on every closed interval \([a,b]\), \(a \lt b\). Furthermore, by Theorem 3, \(f\) must have minimum and maximum values on \([a,b]\).
Note. Theorem 8 is connected to the Intermediate Value Theorem in the following way:
If \(f\colon [a,b]\to \mathbb{R}\) be continuous, then there exist points \(x_1,x_2\in [a,b]\) such that \(f([a,b])=[f(x_1),f(x_2)]\).
4. Derivative
Derivative
The definition of the derivative of a function is given next. We start with an example illustrating the idea behind the formal definition.
Example 0.
The graph below shows how far a cyclist gets from his starting point.
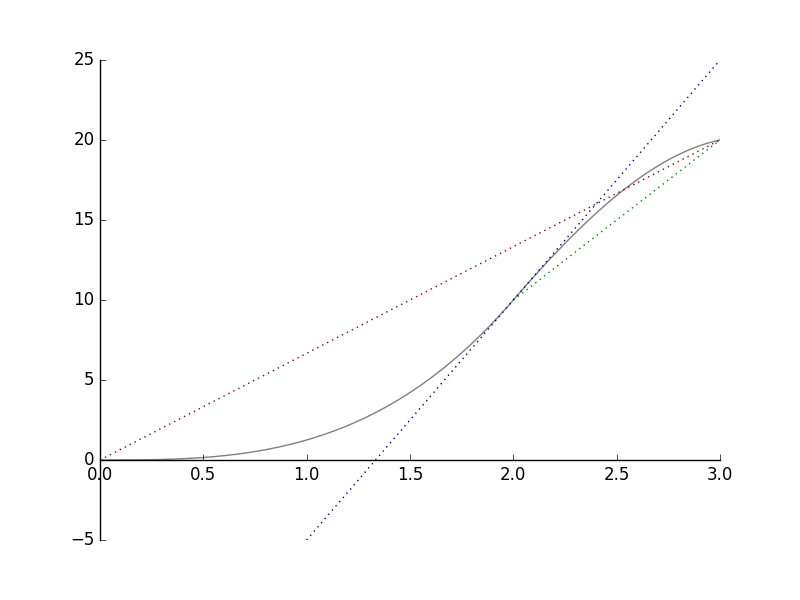
a) Look at the red line. We can see that in three hours, the cyclist moved \(20\)km. The average speed of the whole trip is \(6.6\) km/h.
b) Now look at the green line. We can see that during the third hour the cyclist moved \(10\)km further. That makes the average speed of that time interval \(10\) km/h.
Notice that the slope of the red line is \(20/3 \approx 6.6\) and that the slope of the blue line is \(10\). These are the same values as the corresponding average speeds.
c) Look at the blue line. It is the tangent of the curve at the point \(x=2h\). Using the same principle as with average speeds, we conclude that after two hours of the departure, the speed of the cyclist was \(30/2\) km/h \(= 15\) km/h.
Now we will proceed to the general definition:
Definition: Derivative
Let \((a,b)\subset \mathbb{R}\). The derivative of function \(f\colon (a,b)\to \mathbb{R}\) at the point \(x_0\in (a,b)\) is \[f'(x_0):=\lim_{h\to 0} \frac{f(x_0+h)-f(x_0)}{h}.\] If \(f'(x_0)\) exists, then \(f\) is said to be differentiable at the point \(x_0\).
Note: Since \(x = x_0+h\), then \(h=x-x_0\), and thus the definition can also be written in the form \[f'(x_0):=\lim_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0}.\]
The derivative can be denoted in different ways: \[ f'(x_0)=Df(x_0) =\left. \frac{df}{dx}\right|_{x=x_0}, \ \ f'=Df =\frac{df}{dx}. \]
Interpretation. Consider the curve \(y = f(x)\). Now if we draw a line through the points \((x_0,f(x_0))\) and \((x_0+h, f(x_0+h))\), we see that the slope of this line is \[\frac{f(x_0+h)-f(x_0)}{x_0+h-x_0} = \frac{f(x_0+h)-f(x_0)}{h}.\] When \(h \to 0\), the line intersects with the curve \(y = f(x)\) only in the point \((x_0, f(x_0))\). This line is the tangent of the curve \(y=f(x)\) at the point \((x_0,f(x_0))\) and its slope is \[\lim_{h\to 0} \frac{f(x_0+h)-f(x_0)}{h},\] which is the derivative of the function \(f\) at \( x_0\). Hence, the tangent is given by the equation \[y=f(x_0)+f'(x_0)(x-x_0).\]
Interactivity. Move the point of intersection and observe changes on the tangent line of the curve.
Example 1.
Let \(f\colon \mathbb{R} \to \mathbb{R}\) be the function \(f(x) = x^3 + 1\). The derivative of \(f\) at \(x_0 = 1\) is \[\begin{aligned}f'(1) &=\lim_{h \to 0} \frac{f(1+h)-f(1)}{h} \\ &=\lim_{h \to 0} \frac{(1+h)^3 + 1 - 1^3 - 1}{h} \\ &=\lim_{h \to 0} \frac{1+3h+3h^2+h^3-1}{h} \\ &=\lim_{h \to 0} \frac{h(3+3h+h^2)}{h} \\ &=\lim_{h \to 0} 3+3h+h^2 \\ &= 3. \end{aligned}\]
Function \( x^3 + 1\) and its tangent at the point \(1\).
Example 2.
Let \(f\colon \mathbb{R} \to \mathbb{R}\) be the function \(f(x)=ax+b\). We find the derivative of \(f(x)\).
Immediately from the definition we get: \[\begin{aligned}f'(x) &=\lim_{h\to 0} \frac{f(x+h)-f(x)}{h} \\ &=\lim_{h\to 0} \frac{[a(x+h)+b]-[ax+b]}{h} \\ &=\lim_{h\to 0} a \\ &=a.\end{aligned}\]
Here \(a\) is the slope of the tangent line. Note that the derivative at \(x\) does not depend on \(x\) because \(y=ax+b\) is the equation of a line.
Note. When \(a=0\), we get \(f(x) = b\) and \(f'(x) = 0\). The derivative of a constant function is zero.
Example 3.
Let \(g\colon \mathbb{R} \to \mathbb{R}\) be the function \(g(x)=|x|\). Does \(g\) have a derivative at \(0\)?
Now \[g'(x_0)= \begin{cases}+1 & \text{when $x_{0}>0$} \\ -1 & \text{when $x_{0}<0$}\end{cases}\]
The graph \(y=g(x)\) has no tangent at the point \(x_0=0\): \[\frac{g(0+h)-g(0)}{h}= \frac{|0+h|-|0|}{h}=\frac{|h|}{h}=\begin{cases}+1 & \text{for $h>0$}, \\ -1 & \text{for $h<0$}.\end{cases}\] Thus \(g'(0)\) does not exist.
Conclusion. The function \(g\) is not differentiable at the point \(0\).
Remark. Let \(f\colon (a,b)\to \mathbb{R}\). If \(f'(x)\) exists for every \(x\in (a,b)\) then we get a function \(f'\colon (a,b)\to \mathbb{R}\). We write:
| (1) | \(f(x)\) | = \(f^{(0)}(x)\), | |
| (2) | \(f'(x)\) | = \(f^{(1)}(x)\) | = \(\frac{d}{dx}f(x)\), |
| (3) | \(f''(x)\) | = \(f^{(2)}(x)\) | = \(\frac{d^2}{dx^2}f(x)\), |
| (4) | \(f'''(x)\) | = \(f^{(3)}(x)\) | = \(\frac{d^3}{dx^3}f(x)\), |
| ... |
Here \(f''(x)\) is called the second derivative of \(f\) at \(x\), \(f^{(3)}\) is the third derivative, and so on.
We introduce the notation \begin{eqnarray} C^n\bigl( ]a,b[\bigr) =\{ f\colon \, ]a,b[\, \to \mathbb{R} & \mid & f \text{ is } n \text{ times differentiable on the interval } ]a,b[ \nonumber \\ & & \text{ and } f^{(n)} \text{ is continuous}\}. \nonumber \end{eqnarray} These functions are said to be n times continuously differentiable.
Function \(|x|\).
Example 4.
The distance moved by a cyclist (or a car) is given by \(s(t)\). Then the speed at the moment \(t\) is \(s'(t)\) and the acceleration is \(s''(t)\).
Linearization and differential
Properties of derivative
Next we give some useful properties of the derivative. These properties allow us to find derivatives for some familiar classes of functions such as polynomials and rational functions.
Continuity and derivative
If \(f\) is differentiable at the point \(x_0\), then \(f\) is continuous at the point \(x_0\): \[ \lim_{h\to 0} f(x_0+h) = f(x_0).\] Why? Because if \(f\) is differentiable, then we get \[f(x_0)+h\frac{f(x_0+h)-f(x_0)}{h} \rightarrow f(x_0)+0\cdot f'(x_0)=f(x_0),\] as \(h \to 0\).
Note. If a function is continuous at the point \(x_0\), it doesn't have to be differentiable at that point. For example, the function \(g(x) = |x|\) is continuous, but not differentiable at the point \(0\).
Differentiation Rules
Next we will give some important rules which are often applied in practical problems concerning determination of the derivative of a given function.
Suppose that \(f\) and \(g\) are differentiable at \(x\).
A Constant Multiplier
\[(cf)'(x) = cf'(x),\ c \in \mathbb{R}\]
Suppose that \(f\) is differentiable at \(x\). We determine: \[(cf)'(x),\] where \(c\in \mathbb{R}\) is a constant.
\[\begin{aligned}\frac{(cf)(x+h)-(cf)(x)}{h} \ & \ = \ \frac{cf(x+h)-cf(x)}{h} \\ & \ = \ c \ \frac{f(x+h)-f(x)}{h}\end{aligned}\]
As \(h\to 0\), we get \[c \ \frac{f(x+h)-f(x)}{h} \to c f'(x).\]
\(\square\)
The Sum Rule
\[(f+g)'(x) = f'(x) + g'(x)\]
Suppose that \(f\) and \(g\) are differentiable at \(x\). We determine \[(f+g)'(x).\]
By the definition: \[\begin{aligned}\frac{(f+g)(x+h)-(f+g)(x)}{h} \ & \ = \ \frac{[f(x+h)+g(x+h)]-[f(x)+g(x)]}{h} \\ & \ = \ \frac{f(x+h)-f(x)}{h}+\frac{g(x+h)-g(x)}{h}\end{aligned}\]
When \(h\to 0\), we get \[\frac{f(x+h)-f(x)}{h}+\frac{g(x+h)-g(x)}{h}\to \ f'(x)+g'(x)\]
\(\square\)
The Product Rule
\[(fg)'(x) = f'(x)g(x) + f(x)g'(x)\]
Suppose that \(f,g\) and are differentiable at \(x\). We determine \[(fg)'(x).\] \[\begin{aligned}\frac{(fg)(x+h)-(fg)(x)}{h} & = \frac{f(x+h)g(x+h)-f(x)g(x)}{h} \\ & = \frac{f(x+h)g(x+h)-f(x)g(x+h)+f(x)g(x+h)-f(x)g(x)}{h} \\ & = \frac{f(x+h)-f(x)}{h}\ g(x+h)+f(x)\ \frac{g(x+h)-g(x)}{h}\end{aligned}\]
When \(h\to 0\), we get \[\frac{f(x+h)-f(x)}{h}g(x+h)+f(x)\frac{g(x+h)-g(x)}{h}\to f'(x)g(x)+f(x)g'(x).\]
\(\square\)
The Power Rule
\[\frac{d}{dx} x^n = nx^{n-1} \text{, } n \in \mathbb{Z}\]
For \( n\ge 1\) we repeteadly apply the product rule, and obtain \[\begin{aligned}\frac{d}{dx}x^n \ & = \frac{d}{dx}(x\cdot x^{n-1}) \\ & = (\frac{d}{dx}x)x^{n-1}+x\frac{d}{dx}x^{n-1} \\ & \stackrel{dx/dx=1}{=} x^{n-1}+x\frac{d}{dx}x^{n-1} \\ & = x^{n-1}+x\left( x^{n-2}+x\frac{d}{dx}x^{n-2}\right) \\ & = \ldots \\ & = \sum_{k=0}^{n-1} x^{n-1} \\ & = nx^{n-1}.\end{aligned}\]
The case of negative \( n\) is obtained from this and the product rule applied to the identity \( x^n \cdot x^{-n} = 1\).
From the power rule we obtain a formula for the derivative of a polynomial. Let \[P(x)=a_n x^{n}+a_{n-1}x^{n-1}+\ldots+ a_1 x + a_0,\] where \(n\in \mathbb{N}\). Then \[\frac{d}{dx}P(x)=na_nx^{n-1}+(n-1)a_{n-1}x^{n-2}+\ldots +2 a_2 x+a_1.\]
\(\square\)
The Reciprocal Rule
\[\Big(\frac{1}{f}\Big)'(x) = - \frac{f'(x)}{f(x)^2} \text{, } f(x) \neq 0\]
Suppose that \(f\) is differentiable at \(x\) and \(f(x)\neq 0\). We determine \[(\frac{1}{f})'(x).\]
From the definition we obtain: \[\begin{aligned}\frac{(1/f)(x+h)-(1/f)(x)}{h} & = \frac{1/f(x+h)-1/f(x)}{h} \\ & = \frac{\frac{f(x)}{f(x)f(x+h)}-\frac{f(x+h)}{f(x)f(x+h)}}{h} \\ & = \frac{f(x)-f(x+h)}{h}\frac{1}{f(x)f(x+h)}\end{aligned}\]
Because \(f\) is differentiable at \(x\) we get \[\frac{f(x)-f(x+h)}{h}\frac{1}{f(x)f(x+h)}=-f'(x)/f(x)^2,\] as \(h\to 0\).
\(\square\)
The Quotient Rule
\[(f/g)'(x) = \frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2},\ g(x) \neq 0\]
Suppose that \(f,g\) are differentiable at \(x\) and \(g(x)\neq 0\). Then \[\begin{aligned}(f/g)'(x) & = \Big( f \cdot \frac{1}{g}\Big) '(x) \\ & = f'(x)\frac{1}{g(x)}-f(x)\frac{g'(x)}{g(x)^2} \\ & = \frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}.\end{aligned}\]
\(\square\)
Interactivity. Vary \(x\) and the constant multiplier and see the effect of constant multiplier rule in practice.
Example 1.
\[\frac{d}{dx}(x^{2006}+5x^3+42)=\frac{d}{dx}x^{2006}+5\frac{d}{dx}x^3+42\frac{d}{dx}1=2006x^{2005}+5\cdot 3x^2.\]
Example 2.
\[\begin{aligned}\frac{d}{dx} [(x^4-2)(2x+1)] &= \frac{d}{dx}(x^4-2) \cdot (2x+1) + (x^4-2) \cdot \frac{d}{dx}(2x + 1) \\ &= 4x^3(2x+1) + 2(x^4-2) \\ &= 8x^4+4x^3+2x^4-4 \\ &= 10x^4+4x^3-4.\end{aligned}\]
Note. We can check the answer by deriving it in another way: \[\frac{d}{dx} [(x^4-2)(2x+1)] = \frac{d}{dx} (2x^5 +x^4 -4x -2) = 10x^4 +4x^3 -4.\]
Function \( (x^4-2)(2x+1) \).
Example 3.
For \(x \neq 0\) we get \[\frac{d}{dx} \frac{3}{x^3} = 3 \cdot \frac{d}{dx} \frac{1}{x^3} = -3 \cdot \frac{\frac{d}{dx} x^3}{(x^3)^2} = -3 \cdot \frac{3x^2}{x^6}= - \frac{9}{x^4}.\]
Note. There is another way of solving the problem above by noticing that \(\frac{1}{x^3} = x^{-3}\) and differentiating it as a power: \[\frac{d}{dx} \ \frac{3}{x^3} = 3 \cdot \frac{d}{dx} x^{-3} = 3 \cdot (-3x^{-4})= - \frac{9}{x^4}\]
Example 4.
\[\begin{aligned}\frac{d}{dx} \frac{x^3}{1+x^2} & = \frac{(\frac{d}{dx}x^3)(1+x^2)-x^3\frac{d}{dx}(1+x^2)}{(1+x^2)^2} \\ & = \frac{3x^2(1+x^2)-x^3(2x)}{(1+x^2)^2} \\ & = \frac{3x^2+x^4}{(1+x^2)^2}.\end{aligned}\]
Function \(x^3 / (1+x^2)\).
Rolle's Theorem
If \(f\) is differentiable at a local extremum \(x_0\in \, ]a,b[\), then \(f'(x_0)=0\).
The one-sided limits of the difference quotient have different signs at a local extremum. For example, for a local maximum it holds that \begin{eqnarray} \frac{f(x_0+h)-f(x_0)}{h} = \frac{\text{negative} }{\text{positive}}&\le& 0, \text{ when } h>0, \nonumber \\ \frac{f(x_0+h)-f(x_0)}{h} = \frac{\text{negative}}{\text{negative}}&\ge& 0, \text{ when } h<0 \nonumber \end{eqnarray} and \(|h|\) is so small that \(f(x_0)\) is a maximum on the interval \([x_0-h,x_0+h]\).
L'Hospital's Rule
There are many different versions of this rule, but we present only the simplest one. Let us assume that \(f(x_0)=g(x_0)=0\) and the functions \(f,g\) are differentiable on some interval \(]x_0-\delta,x_0+\delta[\). If \[ \lim_{x\to x_0}\frac{f'(x)}{g'(x)} \] exists, then \[ \lim_{x\to x_0}\frac{f(x)}{g(x)}=\lim_{x\to x_0}\frac{f'(x)}{g'(x)}. \]
In the special case \(g'(x_0)\neq 0\) the proof is simple: \[ \frac{f(x)}{g(x)}=\frac{f(x)-f(x_0)}{g(x)-g(x_0)} = \frac{\bigl( f(x)-f(x_0)\bigr) /(x-x_0)}{\bigl( g(x)-g(x_0)\bigr) /(x-x_0)} \to \frac{f'(x_0)}{g'(x_0)}. \] In the general case we need the so-called generalized mean value theorem, which states that \[ \frac{f(x)}{g(x)} = \frac{f'(c)}{g'(c)} \] for some \(c\in \, ]x_0,x[\). Here we have the same point \(c\) both in the numerator and the denominator, so we do not even need the continuity of the derivatives!
Derivatives of Trigonometric Functions
In this section, we give differentiation formulas for trigonometric functions \(\sin\), \(\cos\) and \(\tan\).
Derivative of Sine
\[\sin'(t)=\cos(t)\]
Function \(\sin(x)\) and its derivative function \(\cos(x)\).
Derivative of Cosine
\[\cos'(t)= - \sin(t)\]
This follows in a similar way as the derivative of Sine, but more easily from the identity \(\cos(t)=\sin(\pi/2-t)\) and the Chain rule to be introduced in the following section.
\(\square\)
Function \(\cos(x)\) and its derivative function \(-\sin(x)\).
Derivative of Tangent
\[\tan'(t) = \frac{1}{\cos^2(t)}=1+\tan^2 t.\]
Because \[\tan(t)=\frac{\sin(t)}{\cos(t)},\] from the quotient rule we obtain \[\tan'(t)=\frac{\sin'(t)\cos(t)-\sin(t)\cos'(t)}{\cos^2(t)}=\frac{\cos^2(t)+\sin^2(t)}{\cos^2(t)}=\begin{cases}\frac{1}{\cos^2(t)} & \\ 1+\tan^2 t.\end{cases}\]
\(\square\)
Function \(\tan(x)\) and its derivative function \(1/\cos^2(x)\).
Example 1.
\[\frac{d}{dx} (3 \sin(x)) = 3 \sin'(x) = 3 \cos(x).\]
Example 2.
\[\frac{d}{dx} \cos^2 (x) = \cos'(x) \cdot \cos(x) + \cos(x) \cdot \cos'(x) = -2\sin(x)\cos(x).\]
Example 3.
\[\begin{aligned} \frac{d}{dx} \frac{\sin(x) + 1}{\cos(x)} &= \frac{d}{dx} \left( \frac{\sin(x)}{\cos(x)} + \frac{1}{\cos(x)} \right) \\ &= \tan'(x) - \frac{\cos'(x)}{\cos^2(x)} \\ &= \frac{1+\sin(x)}{\cos^2 (x)}.\end{aligned}\]
The Chain Rule
In this section we learn a formula for finding the derivative of a composite function. This important formula is known as the Chain Rule.
The Chain Rule.
Let \(f\colon \mathbb{R}\to \mathbb{R}\), \(g\colon \mathbb{R}\to \mathbb{R}\) and \(f \circ g \colon \mathbb{R}\to \mathbb{R}\).
Let \(g\) be differentiable at the point \(x\) and \(f\) at \(g(x)\). Then
\[\frac{d}{dx}f(g(x))=f'(g(x))g'(x).\]
Consider
\[\begin{aligned}\frac{f(g(x+h))-f(g(x))}{h} &= \frac{f(g(x+h))-f(g(x))}{h} \ \frac{g(x+h)-g(x)}{g(x+h)-g(x)} \\ &= \frac{f(g(x+h))-f(g(x))}{g(x+h)-g(x)} \ \frac{g(x+h)-g(x)}{h}.\end{aligned}\]
Now let us write \(k(h):=g(x+h)-g(x)\). Then \(g(x+h)=g(x)+k(h)\) and we get \[\frac{f(g(x+h))-f(g(x))}{h}=\frac{f(g(x)+k(h))-f(g(x))}{k(h)}\frac{g(x+h)-g(x)}{h}.\]
Problem. What if \(k(h)=0\)? Note that one cannot divide by zero.
Solution. Define \[E(k):= \begin{cases}0, & \text{for $k=0$}, \\ \frac{f(g(x)+k)-f(g(x))}{k}-f'(g(x)), & \text{for $k\neq 0$},\end{cases}\] so that \[\frac{f(g(x+h))-f(g(x))}{h}=[E(k(h))+f'(g(x))]\frac{g(x+h)-g(x)}{h}.\] Now, because \(E\) is continuous, we get \[[E(k(h))+f'(g(x))]\frac{g(x+h)-g(x)}{h}\to f'(g(x))g'(x).\] as \(h\to 0\).
\(\square\)
Example 1.
The problem is to differentiate the function \((2x-1)^3\). We take \(f(x) = x^3\) and \(g(x) = 2x-1\) and differentiate the composite function \(f(g(x))\). As \[f'(x) = 3x^2 \text{ and } g'(x) = 2,\] we get \[\frac{d}{dx} (2x-1)^3 = 3(2x-1)^2 \cdot 2 = 6(4x^2-4x+1) = 24x^2-24x+6.\]
Function \((2x-1)^3\) and its derivative function.
Example 2.
We need to differentiate the function \(\sin 3x\). Take \(f(x) = \sin x\) and \(g(x) = 3x\), then differentiate the composite function \(f(g(x))\). \[\frac{d}{dx} \sin 3x = \cos 3x \cdot 3 = 3 \cos 3x.\]
Remark. Let \(h\colon \mathbb{R}\to \mathbb{R}, g\colon \mathbb{R}\to \mathbb{R}\) and \(f\colon \mathbb{R}\to \mathbb{R}\). Now \[\frac{d}{dx}f(g(h(x)))=f'(g(h(x)))\frac{d}{dx}g(h(x))=f'(g(h(x)))g'(h(x))h'(x).\] Similarly, one may obtain even more complex rules for composites of multiple functions.
Function \(\sin 3x\) and its derivative function.
Example 3.
Differentiate the function \(\cos^3 2x\). Take \(f(x) = x^3\), \(g(x) = \cos x\) and \(h(x) = 2x\) and differentiate the composite function \(f(g(h(x)))\). \[\begin{aligned}\frac{d}{dx} \cos^3 2x &= 3(\cos 2x)^2 \cdot \frac{d}{dx} \cos 2x \\ &= 3 \cos^2 2x \cdot (-\sin 2x) \cdot 2 \\ &= -6 \sin 2x \cos^2 2x.\end{aligned}\]
Function \(\cos^3 2x\) and its derivative function.
Extremal Value Problems
We will discuss the Intermediate Value Theorem for differentiable functions, and its connections to extremal value problems.
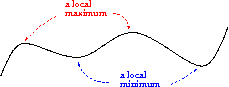
Definition: Local Maxima and Minima
A function \(f\colon A\to \mathbb{R}\) has a a local maximum at the point \(x_0\in A\), if for some \(h\gt 0\) and for all \(x\in A\) such that \(|x-x_0|\lt h\), we have \(f(x)\leq f(x_0)\).
Similarly, a function \(f\colon A\to \mathbb{R}\) has a local minimum at the point \(x_0\in A\) , if for some \(h>0\) and for all \(x\in A\) such that \(|x-x_0|\lt h\), we have \(f(x)\geq f(x_0)\).
A local extreme is a local maximum or a local minimum.
Remark. If \(x_0\) is a local maximum value and \(f'(x_0)\) exists, then \[\begin{cases}f'(x_0) & =\lim_{h\to 0^{+}}\frac{f(x_0+h)-f(x_0)}{h} \leq 0 \\ f'(x_0) & =\lim_{h\to 0^{-}}\frac{f(x_0+h)-f(x_0)}{h} \geq 0.\end{cases}\] Hence \(f'(x_0)=0\).
We get:
Theorem 1.
Let \(x_0\in [a,b]\) be a local extremal value of a continuous function \(f\colon [a,b]\to \mathbb{R}\). Then either
the derivative \(f'(x_0)\) doesn't exist (this includes also cases \(x_0=a\) and \(x_0=b\)) or
\(f'(x_0)=0\).
Example 1.
Let \(f: \mathbb{R} \to \mathbb{R}\) be defined by \[f(x) = x^3 -3x + 1.\] Then \[f'(x) = 3x^2-3\] and we can see that at the points \(x_0 = -1\) and \(x_0 = 1\) the local maximum and minimum of \(f\) are obtained, \[f'(-1) = 3 \cdot (-1)^2 - 3 = 0 \text{ and } f'(1) = 3 \cdot 1^2 - 3 = 0.\]
Function \(x^3-3x+1\) and its derivative function \(3x^2-3\).
Finding the global extrema
In practice, when we are looking for the local extrema of a given function, we need to check three kinds of points:
the zeros of the derivative
the endpoints of the domain of definition (interval)
points where the function is not differentiable
If we happened to know beforehand that the function has a minimum/maximum, then we start off by finding all the possible local extrema (the points described above), evaluate the function at these points and pick the greatest/smallest of these values.
Example 2.
Let us find the smallest and greatest value of the function \(f\colon [0,2]\to \mathbf{R}\), \(f(x)=x^3-6x\). Since the function is continuous on a closed interval, then it has a maximum and a minimum. Since the function is differentiable, it is sufficient to examine the endpoints of the interval and the zeros of the derivative that are contained in the interval.
The zeros of the derivative: \(f'(x)=3x^2-6=0 \Leftrightarrow x=\pm \sqrt{2}\). Since \(-\sqrt{2}\not\in [0,2]\), we only need to evaluate the function at three points, \(f(0)=0\), \(f(\sqrt{2})=-4\sqrt{2}\) and \(f(2)=-4\). From these we can see that the smallest value of the function is \(-4\sqrt{2}\) and the greatest value is \(0\), respectively.
Next we will formulate a fundamental result for differentiable functions. The basic idea here is that the change on an interval can only happen, if there is change at some point on the inverval.
Theorem 2.
(The Intermediate Value Theorem for Differentiable Functions). Let \(f\colon [a,b]\to \mathbb{R}\) be continuous in the interval \([a,b]\) and differentiable in the interval \((a,b)\). Then \[f'(x_0)=\frac{f(b)-f(a)}{b-a}\] for some \(x_0\in (a,b).\)
Let \(f\) be continuous in the interval \([a,b]\) and differentiable in the interval \((a,b)\). Let us define \[g(x):=f(x)-\frac{f(b)-f(a)}{b-a}(x-a)-f(a).\]
Now \(g(a)=g(b)=0\) and \(g\) is differentiable in the interval \((a,b)\). According to Rolle's Theorem, there exists \(c\in(a,b)\) such that \(g'(c)=0\). Hence \[f'(c)=g'(c)+\frac{f(b)-f(a)}{b-a}=\frac{f(b)-f(a)}{b-a}.\]
\(\square\)
This result has an important application:
Theorem 3.
Let \(f\colon (a,b)\to \mathbb{R}\) be a differentiable function. Then
If for all \(x\in (a,b) \ \ f'(x)\geq 0\), then \(f\) is increasing,
If for all \(x\in (a,b) \ \ f'(x)\leq 0\), then \(f\) is decreasing.
Suppose that \(a \lt x_1 \lt x_2 \lt b\).
Then by Theorem 2 there exists \(x_0\in (x_1,x_2)\) such that \[f'(x_0)=\frac{f(x_2)-f(x_1)}{x_2-x_1}.\]
It follows that \(f(x_2)-f(x_1)=f'(x_0)(x_2-x_1)\).
Hence we may conclude that \(f\) is increasing for \(f'(x_0)\geq 0\) and decreasing for \(f'(x_0)\leq 0\).
Example 3.
For the polynomial \(f(x) = \frac{1}{4} x^4-2x^2-7\) the derivative is \[f'(x) = x^3-4x = x(x^2-4) = 0,\] when \(x=0\), \(x=2\) or \(x=-2\). Now we can draw a table:
| \(x<-2\) | \(-2 \lt x \lt 0\) | \(0 \lt x \lt 2\) | \(x>2\) | |
|---|---|---|---|---|
| \(x\) | \(<0\) | \(<0\) | \(>0\) | \(>0\) |
| \(x^2-4\) | \(>0\) | \(<0\) | \(<0\) | \(>0\) |
| \(f'(x)\) | \(<0\) | \(>0\) | \(<0\) | \(>0\) |
| \(f(x)\) | decr. | incr. | decr. | incr. |
Function \(\frac{1}{4} x^4-2x^2-7\).
Example 4.
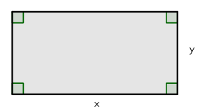
We need to find a rectangle so that its area is \(9\) and it has the least possible perimeter.
Let \(x\ (>0)\) and \(y\ (>0)\) be the sides of the rectangle. Then \(x \cdot y = 9\) and we get \(y=\frac{9}{x}\). Now the perimeter is \[2x+2y = 2x+2 \frac{9}{x} = \frac{2x^2+18}{x}.\] In which point does the function \(f(x) = \frac{2x^2+18}{x}\) get its minimum value? Function \(f\) is continuous and differentiable, when \(x>0\) and using the quotient rule, we get \[f'(x) = \frac{4x \cdot x-(2x^2+18) \cdot 1}{x^2} = \frac{2x^2-18}{x^2}.\] Now \(f'(x) = 0\), when \[\begin{aligned}2x^2-18 &= 0 \\ 2x^2 &= 18 \\ x^2 &= 9 \\ x &= \pm 3\end{aligned}\] but we have defined that \(x>0\) and therefore are only interested in the case \(x=3\). Let's draw a table:
| \(x<3\) | \(x>3\) | |
|---|---|---|
| \(f'(x)\) | \(<0\) | \(>0\) |
| \(f(x)\) | decr. | incr. |
As the function \(f\) is continuous, we now know that it attains its minimum at the point \(x=3\). Now we calculate the other side of the rectangle: \(y=\frac{9}{x}=\frac{9}{3}=3\).
Thus, the rectangle, which has the least possible perimeter is actually a square, which sides are of the length \(3\).
Function \(\frac{2x^2+18}{x}\).
Example 5.
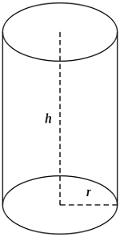
We must make a one litre measure, which is shaped as a right circular cylinder without a lid. The problem is to find the best size of the bottom and the height so that we need the least possible amount of material to make the measure.
Let \(r > 0\) be the radius and \(h > 0\) the height of the cylinder. The volume of the cylinder is \(1\) dm\(^3\) and we can write \(\pi r^2 h = 1\) from which we get \[h = \frac{1}{\pi r^2}.\]
The amount of material needed is the surface area \[A_{\text{bottom}} + A_{\text{side}} = \pi r^2 + 2 \pi r h = \pi r^2 + \frac{2 \pi r}{\pi r^2} = \pi r^2 + \frac{2}{r}.\]
Let function \(f: (0, \infty) \to \mathbb{R}\) be defined by \[f(r) = \pi r^2 + \frac{2}{r}.\] We must find the minimum value for function \(f\), which is continuous and differentiable, when \(r>0\). Using the reciprocal rule, we get \[f'(r) = 2\pi r -2 \cdot \frac{1}{r^2} = \frac{2\pi r^3 - 2}{r^2}.\] Now \(f'(r) = 0\), when \[\begin{aligned}2\pi r^3 - 2 &= 0 \\ 2\pi r^3 &= 2 \\ r^3 &= \frac{1}{\pi} \\ r &= \frac{1}{\sqrt[3]{\pi}}.\end{aligned}\]
Let's draw a table:
| \(r<\frac{1}{\sqrt[3]{\pi}}\) | \(r>\frac{1}{\sqrt[3]{\pi}}\) | |
|---|---|---|
| \(f'(r)\) | \(<0\) | \(>0\) |
| \(f(r)\) | decr. | incr. |
As the function \(f\) is continuous, we now know that it gets its minimum value at the point \(r= \frac{1}{\sqrt[3]{\pi}} \approx 0.683\). Then \[h = \frac{1}{\pi r^2} = \frac{1}{\pi \left(\frac{1}{\sqrt[3]{\pi}}\right)^2} = \frac{1}{\frac{\pi}{\pi^{2/3}}} = \frac{1}{\sqrt[3]{\pi}} \approx 0.683.\]
This means that it would take least materials to make a measure, which is approximately \(2 \cdot 0.683\) dm \( = 1.366\) dm \( \approx 13.7\) cm in diameter and \(0.683\) dm \( \approx 6.8\) cm high.
Function \(\pi r^2 + \frac{2}{r}\).
5. Taylor polynomial
Taylor polynomial
Example
Compare the graph of \(\sin x\) (red) with the graphs of the polynomials \[ x-\frac{x^3}{3!}+\frac{x^5}{5!}-\dots + \frac{(-1)^nx^{2n+1}}{(2n+1)!} \] (blue) for \(n=1,2,3,\dots,12\).
\(\displaystyle\sum_{k=0}^{n}\frac{(-1)^{k}x^{2k+1}}{(2k+1)!}\)
Definition: Taylor polynomial
Let \(f\) be \(k\) times differentiable at the point \(x_{0}\). Then the Taylor polynomial \begin{align} P_n(x)&=P_n(x;x_0)\\\ &=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+ \\ & \dots +\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n\\ &=\sum_{k=0}^n\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k\\ \end{align} is the best polynomial approximation of degree \(n\) (with respect to the derivative) for a function \(f\), close to the point \(x_0\).
Note. The special case \(x_0=0\) is often called the Maclaurin polynomial.
If \(f\) is \(n\) times differentiable at \(x_0\), then the Taylor polynomial has the same derivatives at \(x_0\) as the function \(f\), up to the order \(n\) (of the derivative).
The reason (case \(x_0=0\)): Let \[ P_n(x)=c_0+c_1x+c_2x^2+c_3x^3+\dots +c_nx^n, \] so that \begin{align} P_n'(x)&=c_1+2c_2x+3c_3x^2+\dots +nc_nx^{n-1}, \\ P_n''(x)&=2c_2+3\cdot 2 c_3x\dots +n(n-1)c_nx^{n-2} \\ P_n'''(x)&=3\cdot 2 c_3\dots +n(n-1)(n-2)c_nx^{n-3} \\ \dots && \\ P^{(k)}(x)&=k!c_k + x\text{ terms} \\ \dots & \\ P^{(n)}(x)&=n!c_n \\ P^{(n+1)}(x)&=0. \end{align}
From these way we obtain the coefficients one by one: \begin{align} c_0= P_n(0)=f(0) &\Rightarrow c_0=f(0) \\ c_1=P_n'(0)=f'(0) &\Rightarrow c_1=f'(0) \\ 2c_2=P_n''(0)=f''(0) &\Rightarrow c_2=\frac{1}{2}f''(0) \\ \vdots & \\ k!c_k=P_n^{(k)}(0)=f^{(k)}(0) &\Rightarrow c_k=\frac{1}{k!}f^{(k)}(0). \\ \vdots &\\ n!c_n=P_n^{(n)}(0)=f^{(n)}(0) &\Rightarrow c_k=\frac{1}{n!}f^{(n)}(0). \end{align} Starting from index \(k=n+1\) we cannot pose any new conditions, since \(P^{(n+1)}(x)=0\).
Taylor's Formula
If the derivative \(f^{(n+1)}\) exists and is continuous on some interval \(I=\, ]x_0-\delta,x_0+\delta[\), then \(f(x)=P_n(x;x_0)+E_n(x)\) and the error term \(E_n(x)\) satisfies \[ E_n(x)=\frac{f^{(n+1)}(c)}{(n+1)!}(x-x_0)^{n+1} \] at some point \(c\in [x_0,x]\subset I\). If there is a constant \(M\) (independent of \(n\)) such that \(|f^{(n+1)}(x)|\le M\) for all \(x\in I\), then \[ |E_n(x)|\le \frac{M}{(n+1)!}|x-x_0|^{n+1} \to 0 \] as \(n\to\infty\).
\neq omitted here (mathematical induction or integral).
Examples of Maclaurin polynomial approximations: \begin{align} \frac{1}{1-x} &\approx 1+x+x^2+\dots +x^n =\sum_{k=0}^{n}x^k\\ e^x&\approx 1+x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\dots + \frac{1}{n!}x^n =\sum_{k=0}^{n}\frac{x^k}{k!}\\ \ln (1+x)&\approx x-\frac{1}{2}x^2+\frac{1}{3}x^3-\dots + \frac{(-1)^{n-1}}{n}x^n =\sum_{k=1}^{n}\frac{(-1)^{k-1}}{k}x^k\\ \sin x &\approx x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\dots +\frac{(-1)^n}{(2n+1)!}x^{2n+1} =\sum_{k=0}^{n}\frac{(-1)^k}{(2k+1)!}x^{2k+1}\\ \cos x &\approx 1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\dots +\frac{(-1)^n}{(2n)!}x^{2n} =\sum_{k=0}^{n}\frac{(-1)^k}{(2k)!}x^{2k} \end{align}
Example
Which polynomial \(P_n(x)\) approximates the function \(\sin x\) in the interval \([-\pi,\pi]\) so that the absolute value of the error is less than \(10^{-6}\)?
We use Taylor's Formula for \(f(x)=\sin x\) at \(x_0=0\). Then \(|f^{(n+1)}(c)|\le 1\) independently of \(n\) and the point \(c\). Also, in the interval in question, we have \(|x-x_0|=|x|\le \pi\). The requirement will be satisfied (at least) if \[ |E_n(x)|\le \frac{1}{(n+1)!}\pi^{n+1} < 10^{-6}. \] This inequality must be solved by trying different values of \(n\); it is true for \(n\ge 16\).
The required approximation is achieved with \(P_{16}(x)\), which fo sine is the same as \(P_{15}(x)\).
Check from graphs: \(P_{13}(x)\) is not enough, so the theoretical bound is sharp!
Taylor polynomial and extreme values
If \(f'(x_0)=0\), then also some higher derivatives may be zero: \[ f'(x_0)=f''(x_0)= \dots = f^{(n)}(x_0) =0,\ f^{(n+1)}(x_0) \neq 0. \] Then the behaviour of \(f\) near \(x=x_0\) is determined by the leading term (after the constant term \(f(x_0)\)) \[ \frac{f^{(n+1)}(x_0)}{(n+1)!}(x-x_0)^{n+1}. \] of the Taylor polynomial.
This leads to the following result:
Extreme values
- If \(n\) is even, then \(x_0\) is not an extreme point of \(f\).
- If \(n\) is odd and \(f^{(n+1)}(x_0)>0\), then \(f\) has a local minimum at \(x_0\).
- If \(n\) is odd and \(f^{(n+1)}(x_0)<0\), then \(f\) has a local maximum at \(x_0\).
Newton's method
The first Taylor polynomial \(P_1(x)=f(x_0)+f'(x_0)(x-x_0)\) is the same as the linearization of \(f\) at the point \(x_0\). This can be used in some simple approximations and numerical methods.
Newton's method
The equation \(f(x)=0\) can be solved approximately by choosing a starting point \(x_0\) (e.g. by looking at the graph) and defining \[ x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)} \] for \(n=0,1,2,\dots\) This leads to a sequence \((x_0,x_1,x_2,\dots )\), whose terms usually give better and better approximations for a zero of \(f\).
The recursion formula is based on the geometric idea of finding an approximative zero of \(f\) by using its linearization (i.e. the tangent line).
Example
Find an approximate value of \(\sqrt{2}\) by using Newton's method.
We use Newton's method for the function \(f(x)=x^2-2\) and initial value \(x_0=2\). The recursion formula becomes \[ x_{n+1}= x_n-\frac{x_n^2-2}{2x_n} = \frac{1}{2}\left(x_n+\frac{2}{x_n}\right), \] from which we obtain \(x_1=1{,}5\), \(x_2\approx 1{,}41667\), \(x_3\approx 1{,}4142157\) and so on.
By experimenting with these values, we find that the number of correct decimal places doubles at each step, and \(x_7\) gives already 100 correct decimal places, if intermediate steps are calculated with enough precision.
Taylor series
Taylor series
If the error term \(E_n(x)\) in Taylor's Formula goes to zero as \(n\) increases, then the limit of the Taylor polynomial is the Taylor series of \(f\) (= Maclaurin series for \(x_0=0\)).
The Taylor series of \(f\) is of the form \[ \sum_{k=0}^{\infty}\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k = \lim_{n\to\infty} \sum_{k=0}^{n}\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k . \] This is an example of a power series.
The Taylor series can be formed as soon as \(f\) has derivatives of all orders at \(x_0\) and they are substituted into this formula. There are two problems related to this: Does the Taylor series converge for all values of \(x\)?
Answer: Not always; for example, the function \[ f(x)=\frac{1}{1-x} \] has a Maclaurin series (= geometric series) converging only for \(-1 < x < 1\), although the function is differentiable for all \(x\neq 1\): \[ f(x)=\frac{1}{1-x} = 1+x+x^2+x^3+x^4+\dots \]
If the series converges for some \(x\), then does its sum equal \(f(x)\)? Answer: Not always; for example, the function \[ f(x)=\begin{cases} e^{-1/x^2}, & x\neq 0,\\ 0, & x=0,\\ \end{cases} \] satisfies \(f^{(k)}(0)=0\) for all \(k\in \mathbf{N}\) (elementary but difficult calculation). Thus its Maclaurin series is identically zero and converges to \(f(x)\) only at \(x=0\).
Conclusion: Taylor series should be studied carefully using the error terms. In practice, the series are formed by using some well known basic series.
Examples
\begin{align} \frac{1}{1-x} &= \sum_{k=0}^{\infty} x^k,\ \ |x|< 1 \\ e^x &= \sum_{k=0}^{\infty} \frac{1}{k!}x^k, \ \ x\in \mathbb{R} \\ \sin x &= \sum_{k=0}^{\infty} \frac{(-1)^{k}}{(2k+1)!} x^{2k+1}, \ \ x\in \mathbb{R} \\ \cos x &= \sum_{k=0}^{\infty} \frac{(-1)^{k}}{(2k)!} x^{2k},\ \ x\in \mathbb{R} \\ (1+x)^r &= 1+\sum_{k=1}^{\infty} \frac{r(r-1)(r-2)\dots (r-k+1)}{k!}x^k, |x|<1 \end{align} The last is called the Binomial Series and is valid for all \(r\in \mathbb{R}\). If \(r=n \in \mathbb{N}\), then starting from \(k=n+1\), all the coefficients are zero and in the beginning \[ \binom{n}{k} =\frac{n!}{k!(n-k)!} = \frac{n(n-1)(n-2)\dots (n-k+1)}{k!}. \]
Compare this to the Binomial Theorem: \[ (a+b)^n=\sum_{k=0}^n\binom{n}{k} a^{n-k}b^k =a^n +na^{n-1}b+\dots +b^n \] for \(n\in\mathbb{N}\).
Power series
Definition: Power series
A power series is of the form \[ \sum_{k=0}^{\infty} c_k(x-x_0)^k = \lim_{n\to\infty} \sum_{k=0}^{n}c_k(x-x_0)^k. \] The point \(x_0\) is the centre and the \(c_k\) are the coefficients of the series.
The series converges at \(x\) if the above limit is defined.
There are only three essentially different cases:
Abel's Theorem.
- The power series converges only for \(x=x_0\) (and then it consists of the constant \(c_0\) only)
- The power series converges for all \(x\in \mathbb{R}\)
- The power series converges on some interval \(]x_0-R,x_0+R[\) (and possibly in one or both of the end points), and diverges for other values of \(x\).
The number \(R\) is the radius of convergence of the series. In the first two cases we say that \(R=0\) or \(R=\infty\) respectively.
Example
For which values of the variable \(x\) does the power series \[\sum_{k=1}^{\infty} \frac{k}{2^k}x^k\] converge?
We use the ratio test with \(a_k=kx^k/2^k\). Then \[ \left| \frac{a_{k+1}}{a_k} \right| = \left| \frac{(k+1)x^{k+1}/2^{k+1}}{kx^k/2^k} \right| = \frac{k+1}{2k}|x| \to \frac{|x|}{2} \] as \(k\to\infty\). By the ratio test, the series converges for \(|x|/2<1\), and diverges for \(|x|/2>1\). In the border-line cases \(|x|/2= 1\Leftrightarrow x=\pm 2\) the general term of the series does not tend to zero, so the series diverges.
Result: The series converges for \(-2< x< 2\), and diverges otherwise.
Definition: Sum function
In the interval \(I\) where the series converges, we can define a function \(f\colon I\to \mathbb{R}\) by setting \begin{equation} \label{summafunktio} f(x) = \sum_{k=0}^{\infty} c_k(x-x_0)^k, \tag{1} \end{equation} which is called the sum function of the power series.
The sum function \(f\) is continuous and differentiable on \(]x_0-R,x_0+R[\). Moreover, the derivative \(f'(x)\) can be calculated by differentiating the sum function term by term: \[ f'(x)=\sum_{k=1}^{\infty}kc_k(x-x_0)^{k-1}. \] Note. The constant term \(c_0\) disappears and the series starts with \(k=1\). The differentiated series converges in the same interval \(x\in \, ]x_0-R,x_0+R[\); this may sound a bit surprising because of the extra coefficient \(k\).
Example
Find the sum function of the power series \(1+2x+3x^2+4x^3+\dots\)
This series is obtained by differentiating termwise the geometric series (with \(q=x\)). Therefore, \begin{align} 1+2x+3x^2+4x^3+\dots &= D(1+x+x^2+x^3+x^4+\dots ) \\ &= \frac{d}{dx}\left( \frac{1}{1-x}\right) = \frac{1}{(1-x)^2}. \end{align} Multiplying with \(x\) we obtain \[ \sum_{k=1}^{\infty}kx^{k} = x+2x^2+3x^3+4x^4+\dots = \frac{x}{(1-x)^2}, \] which is valid for \(|x|<1\).
In the case \([a,b]\subset\ ]x_0-R,x_0+R[\) we can also integrate the sum function termwise: \[ \int_a^b f(x)\, dx = \sum_{k=0}^{\infty}c_k\int_a^b (x-x_0)^k\, dx. \] Often the definite integral can be extended up to the end points of the interval of convergence, but this is not always the case.
Example
Calculate the sum of the alternating harmonic series.
Let us first substitute \(q=-x\) to the geometric series. This yields \[ 1-x+x^2-x^3+x^4-\dots =\frac{1}{1-(-x)} = \frac{1}{1+x}. \] By integrating both sides from \(x=0\) to \(x=1\) we obtain \[ 1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\dots =\int_0^1\frac{1}{1+x} =\ln 2. \] Note. Extending the limit of integration all the way up to \(x=1\) should be justified more rigorously here. We shall return to integration later on the course.
6. Elementary functions
This chapter gives some background to the concept of a function. We also consider some elementary functions from a (possibly) new viewpoint. Many of these should already be familiar from high school mathematics, so in some cases we just list the main properties.
Functions
Definition: Function
A function \(f\colon A\to B\) is a rule that determines for each element \(a\in A\) exactly one element \(b\in B\). We write \(b=f(a)\).
Definition: Domain and codomain
In the above definition of a function \(A=D_f\) is the domain (of definition) of the function \(f\) and \(B\) is called the codomain of \(f\).
Definition: Image of a function
The image of \(f\) is the subset
\(f[A]= \{ f(a) \mid a\in A\}\) of \(B\). An alternative name for image is range.
For example, \(f\colon \mathbb{R}\to\mathbb{R}\), \(f(x)=x^2\), has codomain \(\mathbb{R}\), but its image is \(f[\mathbb{R} ] =[0,\infty[\).
The function in the previous example can also be defined as \(f\colon \mathbb{R}\to [0,\infty[\), \(f(x)=x^2\), and then the codomain is the same as the image. In principle, this modification can always be done, but it is not reasonable in practice.
Example: Try to do the same for \(f\colon \mathbb{R}\to\mathbb{R}\), \(f(x)=x^6+x^2+x\), \(x\in\mathbb{R}\).
If the domain \(A\subset \mathbb{R}\) then \(f\) is a function of one (real) variable: the main object of study in this course.
If \(A\subset \mathbb{R}^n\), \(n\ge 2\), then \(f\) is a function of several variables (a multivariable function)
Inverse functions
Definition: Injection, surjection and bijection
A function \(f\colon A \to B\) is- injective (one-to-one) if it has different values at different points; i.e. \[x_1\neq x_2 \Rightarrow f(x_1)\neq f(x_2),\] or equivalently \[f(x_1)= f(x_2) \Rightarrow x_1=x_2.\]
- surjective (onto) if its image is the same as codomain, i.e. \(f[A]=B\)
- bijective (one-to-one and onto) if it is both injective and surjective.
Observe: A function becomes surjective if all redundant points of the codomain are left out. A function becomes injective if the domain is reduced so that no value of the function is obtained more than once.
Another way of defining these concepts is based on the number of solutions to an equation:
Definition
For a fixed \(y\in B\), the equation \(y=f(x)\) has
- at most one solution \(x\in A\) if \(f\) is injective
- at least one solution \(x\in A\) if \(f\) is surjective
- exactly one solution \(x\in A\) if \(f\) on bijective.
Definition: Inverse function
If \(f\colon A \to B\) is bijective, then it has an inverse \(f^{-1}\colon B \to A\), which is uniquely determined by the condition \[y=f(x) \Leftrightarrow x = f^{-1}(y).\]
The inverse satisfies \(f^{-1}(f(a))=a\) for all \(a\in A\) and \(f(f^{-1}(b))=b\) for all \(b\in B\).
The graph of the inverse is the mirror image of the graph of \(f\) with respect to the line \(y=x\): A point \((a,b)\) lies on the graph of \(f\) \(\Leftrightarrow\) \(b=f(a)\) \(\Leftrightarrow\) \(a=f^{-1}(b)\) \(\Leftrightarrow\) the point \((b,a)\) lies on the graph of \(f^{-1}\). The geometric interpretation of \((a,b)\mapsto (b,a)\) is precisely the reflection with respect to \(y=x\).
If \(A \subset \mathbb{R}\) and \(f\colon A\to \mathbb{R}\) is strictly monotone, then the function \(f\colon A \to f[A]\) has an inverse.
If here \(A\) is an interval and \(f\) is continuous, then also \(f^{-1}\) is is continuous in the set \(f[A]\).
Theorem: Derivative of the inverse
Let \(f\colon \, ]a,b[\, \to\, ]c,d[\) be differentiable and bijective, so that it has an inverse \(f^{-1}\colon \, ]c,d[\, \to\, ]a,b[\). As the graphs \(y=f(x)\) and \(y=f^{-1}(x)\) are mirror images of each other, it seems geometrically obvious that also \(f^{-1}\) is differentiable, and we actually have \[ \left(f^{-1}\right)'(x)=\frac{1}{f'(f^{-1}(x))}, \] if \(f'(f^{-1}(x))\neq 0\).
Differentiate both sides of the equation \begin{align} f(f^{-1}(x)) &= x \\ \Rightarrow f'(f^{-1}(x))\left(f^{-1}\right)'(x) &= Dx = 1, \end{align} and solve for \(\left(f^{-1}\right)'(x)\).
\(\square\)
Note. \(f'(f^{-1}(x))\) is the derivative of \(f\) at the point \(f^{-1}(x)\).
Transcendental functions
Trigonometric functions
Unit of measurement of an angle = rad: the arclength of the arc on the unit circle, that corresponds to the angle.
\(\pi\) rad = \(180\) degrees, i.e. \(1\) rad = \(180/\pi \approx 57,\! 3\) degrees
The functions \(\sin x, \cos x\) are defined in terms of the unit circle so that \((\cos x,\sin x)\), \(x\in [0,2\pi]\), is the point on the unit circle corresponding to the angle \(x\in\mathbb{R}\), measured counterclockwise from the point \((1,0)\). \[\tan x = \frac{\sin x}{\cos x}\ (x\neq \pi /2 +n\pi),\] \[\cot x = \frac{\cos x}{\sin x}\ (x\neq n\pi)\]
Periodicity: \[\sin (x+2\pi) = \sin x,\ \cos (x+2\pi)=\cos x,\] \[\tan (x+\pi) = \tan x\]
\(\sin 0 = 0\), \(\sin (\pi/2)=1\)
\(\cos 0=1\), \(\cos (\pi/2)= 0\)
Parity: \(\sin\) and \(\tan\) are odd functions, \(\cos\) is an even function: \[\sin (-x) = -\sin x,\] \[\cos(-x) = \cos x,\] \[\tan (-x) = -\tan x.\]
\(\sin^2 x + \cos^2 x = 1\) for all \(x\in\mathbb{R}\)
Proof: Pythagorean Theorem.
Addition formulas:
\(\sin (x+y) = \sin x \cos y +\cos x \sin y\)
\(\cos (x+y) = \cos x \cos y -\sin x \sin y\)
Basic properties (from the unit circle!)
Proof: Geometrically, or more easily with vectors and matrices.
Derivatives: \[ D(\sin x) = \cos x,\ \ D(\cos x) = -\sin x \]
Example
It follows that the functions \(y(t)=\sin (\omega t)\) and \(y(t)=\cos (\omega t)\) satisfy the differential equation \[ y''(t)+\omega^2y(t)=0, \] that models harmonic oscillation. Here \(t\) is the time variable and the constant \(\omega>0\) is the angular frequency of the oscillation. We will see later that all the solutions of this differential equation are of the form \[ y(t)=A\cos (\omega t) +B\sin (\omega t), \] with \(A,B\) constants. They will be uniquely determined if we know the initial location \(y(0)\) and the initial velocity \(y'(0)\). All solutions are periodic and their period is \(T=2\pi/\omega\).
where \(t\) is the elapsed time in seconds
Arcus functions
The trigonometric functions have inverses if their domain and codomains are chosen in a suitable way.
The Sine function \[ \sin \colon [-\pi/2,\pi/2]\to [-1,1] \] is strictly increasing and bijective.
The Cosine function \[ \cos \colon [0,\pi] \to [-1,1] \] is strictly decreasing and bijective.
The tangent function \[ \tan \colon ]-\pi/2,\pi/2[\, \to \mathbb{R} \] is strictly increasing and bijective.
Arcus functions
Inverses: \[\arctan \colon \mathbb{R}\to \ ]-\pi/2,\pi/2[,\] \[\arcsin \colon [-1,1]\to [-\pi/2,\pi/2],\] \[\arccos \colon [-1,1]\to [0,\pi]\]
This means: \[x = \tan \alpha \Leftrightarrow \alpha = \arctan x \ \ \text{for } \alpha \in \ ]-\pi/2,\pi/2[ \] \[x = \sin \alpha \Leftrightarrow \alpha = \arcsin x \ \ \text{for } \alpha \in \, [-\pi/2,\pi/2] \] \[x = \cos \alpha \Leftrightarrow \alpha = \arccos x \ \ \text{for } \alpha \in \, [0,\pi] \]
The graphs of \(\tan\) and \(\arctan\).
Derivatives of the arcus functions
\[D \arctan x = \frac{1}{1+x^2},\ x\in \mathbb{R} \tag{1}\] \[D\arcsin x = \frac{1}{\sqrt{1-x^2}},\ -1 < x < 1 \tag{2}\] \[D\arccos x = \frac{-1}{\sqrt{1-x^2}},\ -1 < x < 1 \tag{3}\]
Note. The first result is very useful in integration.
Here we will only prove the first result (1). By differentiating both sides of the equation \(\tan(\arctan x)=x\) for \(x\in \mathbb{R}\): \[\bigl( 1+\tan^2(\arctan x)\bigr) \cdot D(\arctan x) = D x = 1\] \[\Rightarrow D(\arctan x)= \frac{1}{1+\tan^2(\arctan x)}\] \[=\frac{1}{1+x^2}.\]
The last row follows also directly from the formula for the derivative of an inverse.
Example
Show that \[ \arcsin x +\arccos x =\frac{\pi}{2} \] for \(-1\le x\le 1\).
Example
Derive the addition formula for tan, and show that \[ \arctan x+\arctan y = \arctan \frac{x+y}{1+xy}. \]
Solutions: Voluntary exercises. The first can be deduced by looking at a rectangular triangle with the length of the hypotenuse equal to 1 and one leg of length \(x\).
Introduction: Radioactive decay
Let \(y(t)\) model the number of radioactive nuclei at time \(t\). During a short time interval \(\Delta t\) the number of decaying nuclei is (approximately) directly proportional to the length of the interval, and also to the number of nuclei at time \(t\): \[ \Delta y = y(t+\Delta t)-y(t) \approx -k\cdot y(t)\cdot \Delta t. \] The constant \(k\) depends on the substance and is called the decay constant. From this we obtain \[ \frac{\Delta y}{\Delta t} \approx -ky(t), \] and in the limit as \(\Delta t\to 0\) we end up with the differential equation \(y'(t)=-ky(t)\).
Exponential function
Definition: Euler's number
Euler's number (or Napier's constant) is defined as \[e = \lim_{n\to \infty} \left( 1+\frac{1}{n}\right) ^n = 1+1+\frac{1}{2!}+\frac{1}{3!} +\frac{1}{4!} +\dots \] \[\approx 2,\! 718281828459\dots\]
Definition: Exponential function
The Exponential function exp: \[ \exp (x) = \sum_{k=0}^{\infty} \frac{x^k}{k!}= \lim_{n\to \infty} \left( 1+\frac{x}{n}\right) ^n = e^x. \] This definition (using the series expansion) is based on the conditions \(\exp'(x)=\exp(x)\) and \(\exp(0)=1\), which imply that \(\exp^{(k)}(0)=\exp(0)= 1\) for all \(k\in\mathbb{N}\), so the Maclaurin series is the one above.
The connections between different expressions are surprisingly tedious to prove, and we omit the details here. The main steps include the following:
Define \(\exp\colon\mathbb{R}\to\mathbb{R}\), \[ \exp (x) =\sum_{k=0}^{\infty}\frac{x^k}{k!}. \] This series converges for all \(x\in\mathbb{R}\) (ratio test).
Show: exp is differentiable and satisfies \(\exp'(x)=\exp(x)\) for all \(x\in \mathbb{R}\). (This is the most difficult part but intutively rather obvious, because in practice we just differentiate the series term by term like a polynomial.)
It has the following properties \(\exp (0)=1\), \[ \exp (-x)=1/\exp (x) \text{ and } \exp (x+y)=\exp (x)\, \exp(y) \] for all \(x,y\in \mathbb{R}\).
These imply that \(\exp (p/q)=(\exp (1))^{p/q}\) for all rational numbers \(p/q\in \mathbf{Q}\).
By continuity \[ \exp (x) =(\exp (1))^x \] for all \(x\in \mathbb{R}\).
Since \[ \exp (1) = \sum_{k=0}^{\infty}\frac{1}{k!} =\lim_{n\to \infty} \left( 1+\frac{1}{n}\right) ^n=e, \] we obtain the form \(e^x\).
\(\square\)?
Corollary
It follows from above that \(\exp\colon\mathbb{R}\to\, ]0,\infty[\) is strictly increasing, bicective, and \[ \lim_{x\to\infty}\exp(x) = \infty,\ \lim_{x\to-\infty}\exp(x) = 0,\ \lim_{x\to\infty}\frac{x^n}{\exp (x)} = 0 \text{ for all } n\in \mathbf{N}. \]
From here on we write \(e^x=\exp(x)\). Properties:
- \(e^0 = 1\)
- \(e^x >0\)
- \(D(e^x) = e^x\)
- \(e^{-x} = 1/e^x\)
- \((e^x)^y = e^{xy}\)
- \(e^xe^y =e^{x+y}\)
Differential equation \(y'=ky\)
Theorem
Let \(k\in\mathbb{R}\) be a constant. All solutions \(y=y(x)\) of the ordinary differenial equation (ODE) \[ y'(x)=ky(x),\ x\in \mathbb{R}, \] are of the form \(y(x)=Ce^{kx}\), where \( C\) is a constant. If we know the value of \(y\) at some point \(x_0\), then the constant \(C\) will be uniquely determined.
Suppose that \(y'(x)=ky(x)\). Then \[D(y(x)e^{-kx})= y'(x)e^{-kx}+y(x)\cdot (-ke^{-kx})\] \[= ky(x)e^{-kx}-ky(x)e^{-kx}=0\] for all \(x\in\mathbf{R}\), so that \(y(x)e^{-kx}=C=\) constant. Multiplying both sides with \(e^{kx}\) we obtain \(y(x)=Ce^{kx}\).
\(\square\)
Euler's formula
Definition: Complex numbers
Imaginary unit \(i\): a strange creature satisfying \(i^2=-1\). The complex numbers are of the form \(z=x+iy\), where \(x,y\in \mathbb{R}\). We will return to these later.
Theorem: Euler's formula
If we substitute \(ix\) as a variable in the expontential fuction, and collect real terms separately, we obtain Euler's formula \[e^{ix}=\cos x+i\sin x.\]
\(\square\)
As a special case we have Euler's identity \(e^{i\pi}+1=0\). It connects the most important numbers \(0\), \(1\), \(i\), \(e\) ja \(\pi\) and the three basic operations sum, multiplication, and power.
Using \(e^{\pm ix}=\cos x\pm i\sin x\) we can also derive the expressions \[ \cos x=\frac{1}{2}\bigl( e^{ix}+e^{-ix}\bigr),\ \sin x=\frac{1}{2i}\bigl( e^{ix}-e^{-ix}\bigr), \ x\in\mathbb{R}. \]
Logarithms
Definition: Natural logarithm
Natural logarithm is the inverse of the exponential function: \[ \ln\colon \ ]0,\infty[ \ \to \mathbb{R} \]
Note. The general logarithm with base \(a\) is based on the condition \[ a^x = y \Leftrightarrow x=\log_a y \] for \(a>0\) and \(y>0\).
Beside the natural logarithm, in applications also appear the Briggs logarithm with base 10: \(\lg x = \log_{10} x\), and the binary logarithm with base 2: \({\rm lb}\, x =\log_{2} x\).
Usually (e.g. in mathematical software) \(\log x\) is the same as \(\ln x\).
Properties of the logarithm:
- \(e^{\ln x} = x\) for \(x>0\)
- \(\ln (e^x) =x\) for \(x\in\mathbb{R}\)
- \(\ln 1=0\), \(\ln e = 1\)
- \(\ln (a^b) = b\ln a\) if \(a>0\), \(b\in\mathbb{R}\)
- \(\ln (ab) = \ln a+\ln b\), if \(a,b>0\)
- \(D\ln |x|=1/x\) for \(x\neq 0\)
These follow from the corresponding properties of exp.
Example
Substituting \(x=\ln a\) and \(y=\ln b\) to the formula
\(e^xe^y =e^{x+y}\) we obtain \(ab =e^{\ln a+\ln b},\)
so that \(\ln (ab) = \ln a +\ln b\).Hyperbolic functions
Definition: Hyperbolic functions
Hyperbolic sine sinus hyperbolicus \(\sinh\), hyperbolic cosine cosinus hyperbolicus \(\cosh\) and hyperbolic tangent \(\tanh\) are defined as \[\sinh \colon \mathbb{R}\to\mathbb{R}, \ \sinh x=\frac{1}{2}(e^x-e^{-x})\] \[\cosh \colon \mathbb{R}\to [1,\infty[,\ \cosh x=\frac{1}{2}(e^x+e^{-x})\] \[\tanh \colon \mathbb{R}\to \ ]-1,1[, \ \tanh x =\frac{\sinh x}{\cosh x}\]
Properties: \(\cosh^2x-\sinh^2x=1\); all trigonometric have their hyperbolic counterparts, which follow from the properties \(\sinh (ix)=i\sin x\), \(\cosh (ix)=\cos x\). In these formulas, the sign of \(\sin^2\) will change, but the other signs remain the same.
Derivatives: \(D\sinh x=\cosh x\), \(D\cosh x=\sinh x\).
Hyperbolic inverse functions: the so-called area functions; area and the shortening ar refer to a certain geometrical area related to the hyperbola \(x^2-y^2=1\): \[\sinh^{-1}x=\text{arsinh}\, x=\ln\bigl( x+\sqrt{1+x^2}\, \bigr) ,\ x\in\mathbb{R} \] \[\cosh^{-1}x=\text{arcosh}\, x=\ln\bigl( x+\sqrt{x^2-1}\, \bigr) ,\ x\ge 1\]
Derivatives of the inverse functions: \[D \sinh^{-1}x= \frac{1}{\sqrt{1+x^2}} ,\ x\in\mathbb{R} \] \[D \cosh^{-1}x= \frac{1}{\sqrt{x^2-1}} ,\ x > 1.\]
7. Area
Table of Content
Area in the plane
We consider areas of plane sets bounded by closed curves. In the more general cases, the concept of area becomes theoretically very difficult.
The area of a planar set is defined by reducing to the areas of simpler sets. The area cannot be "calculated", unless we first have a definition of "area" (although this is common practice in school mathematics).
Starting point
The area of a rectangle
The area of a rectangle is
Definition: Area of a Parallelogram
The area of a parallelogram is
Definition: Area of a triangle
The area of a triangle is (by definition) \[ A=\frac{1}{2}ah. \]
Polygon
A (simple) polygon is a plane set bounded by a closed curve that consists of a finite number of line segments without self-intersections.
Definition: Area of a polygon
The area of a polygon is defined by dividing it into a
finite number of triangles (called a
Theorem.
The sum of the areas of triangles in a triangulation of a polygon is the same for all triangulations.
General case
For a plane set \(\color{red} D\) bounded by a closed curve we can construct inner polygons \(\color{blue}P_i\) and outer polygons \(P_o\): \(\color{blue}P_i\color{black} \subset \color{red}D\color{black}\subset P_o\).
A surprise: The condition that \(D\) is bounded by a closed curve (without self-intersections) does not guarantee that it has an area! Reason: The boundary curve can be so "wiggly", that it has positive "area". The first such example was constucted by [W.F. Osgood, 1903]:
Wikipedia: Osgood curveExample
Derive the formula \(A=\pi R^2\) for a circle with radius \(R\) by choosing regular inscrided and circumscribed \(n\)-gons as inner and outer polygons, and let \(n\to\infty\).
The solution is a voluntary exercise, where you need the limit \[\lim_{x\to 0}\frac{\sin x}{x} = 1.\] Hint: Show that the inscribed and circumscribed areas are \[ \pi R^2\frac{\sin (2\pi/n)}{2\pi/n} \ \text{ and }\ \pi R^2\frac{\tan \pi/n}{\pi/n}.\]
8. Integral
From sum to integral
Definite integral
Geometric interpretation: Let \(f\colon[a,b]\to\mathbb{R}\) be such that \(f(x)\ge 0\) for all \(x\in[a,b]\). How can we find the area of the region bounded by the function graph \(y=f(x)\), the x-axis and the two lines \(x=a\) and \(x=b\)?
The answer to this question is given by the definite integral \[\int_{a}^{b}f(x)\,dx\] Remark. The general definition of the integral does not necessitate the condition \(f(x)\ge 0\).
Integration of continuous functions
Definition: Partition
Let \(f\colon[a,b]\to\mathbb{R}\) be continuous. A finite sequence \(D=(x_{0},x_{1},x_{2},\dots,x_{n})\) of real numbers such that \[a=x_{0} < x_{1} < x_{2} < \dots < x_{n} = b\] is called a partition of the interval \([a,b]\).
Definition: Upper and lower sum
For each partition \(D\) we define the related upper sum of the function \(f\) as \[U_{D}(f) = \sum_{k=1}^{n}M_{k}(x_{k}-x_{k-1}),~M_{k} = \max\{f(x)\mid x_{k-1}\le x\le x_{k}\}\] and the lower sum as \[L_{D}(f) = \sum_{k=1}^{n}m_{k}(x_{k}-x_{k-1}),~m_{k}=\min\{f(x)\mid x_{k-1}\le x\le x_{k}\}.\]
If \(f\) is a positive function then the upper sum represents the total area of the rectangles circumscribing the function graph and similarly the lower sum is the total area of the inscribed rectangles.
Properties of partitions
- Suppose that \(D_{1}\) and \(D_{2}\) are two partitions of a given interval such that \(D_{1}\) is a subsequence of
\(D_{2}\) (i.e. \(D_{2}\) is finer than \(D_{1}\)). Then the inequalities
\(U_{D_1}(f) \ge U_{D_{2}}(f)~\) and \(~L_{D_{1}}(f) \le L_{D_{2}}(f)\)
always hold. - For any two partitions \(D_{1}\) and \(D_{2}\) of a given interval the inequality \[ L_{D_{2}}(f) \le U_{D_{1}}(f)\] always holds.
\(f(x)=~\)
| Upper Darboux sum | Lower Darboux sum |
Definition: Integrability
We say that a function \(f\colon[a,b]\to\mathbb{R}\) is integrable if for every \(\epsilon>0\) there exists a corresponding partition \(D\) of \([a,b]\) such that \[ U_{D}(f) - L_{D}(f) < \epsilon.\]
Definition: Integral
Integrability implies that there exists a unique real number \(I\) such that \(L_{D}(f)\le I\le U_{D}(f)\) for every partition \(D\). This is called the integral of \(f\) over the interval \([a,b]\) and denoted by \[ I = \int_{a}^{b}f(x)\,dx. \]
Remark. This definition of the integral is sometimes referred to as the Darboux integral.
For non-negative functions \(f\) this definition of the integral coincides with the idea of making the difference between the the areas of the circumscribed and the inscribed rectangles arbitrarily small by using ever finer partitions.
Theorem.
A continuous function on a closed interval is integrable.
Here we will only provide the proof for continuous functions with bounded derivatives.
Suppose that \(f\colon[a,b]\to\mathbb{R}\) is a continuous function and that there exists a constant \(L>0\) such that \(|f'(x)|\le L\) for all \(x\in]a,b[\). Let \(\epsilon>0\) and define \(D\) to be an equally spaced partition of \([a,b]\) such that \[\underbrace{|x_{k}-x_{k-1}|}_{=\Delta x} < \frac{\epsilon}{L(b-a)},~\text{for all} k=1,2,\dots,n.\] Let \(f(y_{k})=m_{k}\) and \(f(z_{k})=M_{k}\) for some suitable points \(y_{k},z_{k}\in[x_{k-1},x_{k}]\). The mean value theorem then states that \[M_{k}-m_{k}=f'(c_{k})|z_{k}-y_{k}|\le L\Delta x<\frac{\epsilon}{b-a}.\] and thus \[U_{D}(f)-L_{D}(f) = \sum_{k=1}^{n}(M_{k}-m_{k})\Delta x < \frac{\epsilon}{b-a}\sum_{k=1}^{n}\Delta x = \epsilon.\]
\(\square\)
Definition: Riemann integral
Suppose that \(f\colon[a,b]\to\mathbb{R}\) is a continuous function and let \((x_{0},x_{1},\dots,x_{n})\) be a partition of \(\left[a,b\right]\) and \((z_{1},z_{2},\dots,z_{n})\) be a sequence of real numbers such that \(z_{k}\in[x_{k-1},x_{k}]\) for all \(1\le k\le n\). The partial sums \[ S_{n} = \sum_{k=1}^{n}f(z_{k})\Delta x_{k},~\text{where} ~\Delta x_{k}=x_{k}-x_{k-1} \] are called the Riemann sums of \(f\). Suppose further that the partitions are such that \(\displaystyle\max_{1\le k\le n}\Delta x_{k}\to 0\) as \(n\to\infty\). The integral of \(f\) can then be defined as the limit \[ \int_{a}^{b}f(x)\,\mathrm{d}x = \lim_{n\to\infty} S_{n}. \] This definition of the integral is called the Riemann integral.
Remark. This definition of the integral turns out to be equivalent to that of the Darboux integral i.e. a function is Riemann-integrable if and only if it is Darboux-integrable and the values of the two integrals are always equal.
Example
Find the integral of \(f(x)=x\) over the interval \([0,1]\) using Riemann sums.
Let \(x_{k}=k/n\). Then \(x_{0}=0\), \(x_{n}=1\) and \(x_{k} < x_{k+1}\) for all \(0\le k\le n\). Thus the sequence \((x_{0},x_{1},x_{2},\dots,x_{n})\) is a proper partition of \(\left[0,1\right]\). This partition has the pleasant property hat \(\Delta x=1/n\) is a constant. Estimating the Riemann sums we now find that \[\sum_{k=1}^{n}f(x_{k})\Delta x = \sum_{k=1}^{n}x_{k}\Delta x= \sum_{k=1}^{n}\frac{k}{n}\left(\frac{1}{n}\right)\] \[= \frac{1}{n^2}\sum_{k=1}^{n}k = \frac{1}{n^2}\frac{n(n+1)}{2} = \frac{n+1}{2n}\to \frac{1}{2},\] as \(n\to\infty\) and hence \[\int_{0}^{1}f(x)\,\mathrm{d}x = \frac{1}{2}.\]
This is of course the area of the triangular region bounded by the line \(y=x\), the \(x\)-axis and the lines \(x=0\) and \(x=1\).
Remark. Any interval \([a,b]\) can be partitioned into equally spaced subintervals by setting \(\Delta x = (b-a)/n\) and \(x_{k} = a + k\Delta x\).
Conventions
- If the upper and lower limits of integration are the same then the integral is zero: \[ \int_{a}^{a}f(x)\,dx = 0.\]
- Reversing the limits of integration changes the sign of the integral: \[ \int_{b}^{a}f(x)\,dx = -\int_{a}^{b}f(x)\,dx.\]
- It also follows that \[ \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx \] holds for all \(a,b,c\in\mathbb{R}\).
Piecewise-defined functions
Definition: Piecewise continuity
A function \(f\colon\left[a,b\right]\to\mathbb{R}\) is called piecewise continuous if it is continuous except at a finite number of points \[a\le c_{1} < c_{2} < \dots < c_{m} \le b\] and the one-sided limits of the function are defined and bounded on each of these points. It follows that the restriction of \(f\) on each subinterval \(\left[c_{k-1},c_{k}\right]\) is continuous if the one-sided limits are taken to be the values of the function at the end points of the subinterval.
Definition: Piecewise integration
Let \(f\colon\left[a,b\right]\) be a piecewise continuous function. Then \[\int_{a}^{b}f(x)\,dx = \sum_{k=1}^{m+1}\int_{c_{k-1}}^{c_{k}}f(x)\,dx,\] where \(a=c_{0}< c_{1} < \dots < c_{m+1} = b\) and \(f\) is thought as a continuous function on each subinterval \(\left[c_{k-1},c_{k}\right]\). Usually functions which are continuous yet piecewise defined are also integrated using the same idea.
Example
Consider the function \(f\colon\left[-1,1\right]\) defined as \[ f(x) = \begin{cases} -1 &\text{ for }-1\le x<0 \\ 1 &\text{ for }0\le x\le 1. \end{cases} \] We can now integrate \(f\) as follows: \[ \int_{-1}^{1}f(x)\,dx = \int_{-1}^{0}f(x)\,dx + \int_{0}^{1}f(x)\,dx \] \[ =\int_{-1}^{0}(-1)\,dx + \int_{0}^{1}1\,dx = -1\cdot(-1-0) + 1\cdot(1-0) = 2. \]
Important properties
Properties
Suppose that \(f,g\colon\left[a,b\right]\to\mathbb{R}\) are piecewise continuous functions. The integral has the following properties
- Linearity: If \(c_{1},c_{2}\in\mathbb{R}\) then \[\int_{a}^{b}\big(c_{1}f(x)+c_{2}g(x)\big)\,\mathrm{d}x = c_{1}\int_{a}^{b}f(x)\,\mathrm{d}x+c_{2}\int_{a}^{b}g(x)\,\mathrm{d}x.\]
- If \(h(x)\ge 0\) for all \(x\in[a,b]\) then \[\int_{a}^{b}h(x)\,\mathrm{d}x \ge 0.\]
- If \(f(x)\le g(x)\) then \[\int_{a}^{b}f(x)\,\mathrm{d}x \le \int_{a}^{b}g(x)\,\mathrm{d}x.\]
- As \(f(x)\le|f(x)|\) it follows that \[\int_{a}^{b}f(x)\,\mathrm{d}x \le \int_{a}^{b}|f(x)|\,\mathrm{d}x\] and taking the absolute value of both sides of the equation gives \[\left|\int_{a}^{b}f(x)\,\mathrm{d}x\right|\le \int_{a}^{b}|f(x)|\,\mathrm{d}x.\]
- Suppose that \(p=\inf_{x\in\left[a,b\right]}f(x)\) and \(s=\sup_{x\in\left[a,b\right]}f(x)\). Then \[p(b-a)\le \int_{a}^{b}f(x)\,dx \le s(b-a).\]
Fundamental theorem of calculus
Theorem: Mean value theorem
Let \(f\colon[a,b]\to\mathbb{R}\) be a continuous function. Then there exists \(c\in(a,b)\) such that \[ f(c)=\frac{1}{b-a}\int_{a}^{b}f(x)\,\mathrm{d}x.\] This is the mean value of \(f\) on the interval \([a,b]\) and we denote it with \(\overline{f}\).
Suppose that \(m\) and \(M\) are the minimum and maximum of \(f\) on the interval \([a,b]\), respectively. It follows that \[ m(b-a)\le \int_{a}^{b}f(x)\,\mathrm{d}x\le M(b-a)\] or \[m\le \frac{1}{b-a}\int_{a}^{b}f(x)\,\mathrm{d}x\le M\quad \Leftrightarrow\quad m\le \overline{f}\le M.\] Thus \(\overline{f}\) is between the minimum and maximum of a continuous function \(f\) and by the intermediate value theorem it must be that \(f(c)=\overline{f}\) for some \(c\in\,]a,b[\).
\(\square\)
(First) Fundamental theorem of calculus.
Let \(f\colon[a,b]\to\mathbb{R}\) be a continuous function. Then \[ \frac{\mathrm{d}}{\mathrm{d}x}\int_{a}^{x}f(t)\,\mathrm{d}t = f(x)\] for all \(x\in\,]a,b[\).
Let \[ F(x) = \int_{a}^{x}f(t)\,\mathrm{d}t. \] The mean value theorem implies that there exists \(c\in\,[x,x+h]\) such that \[ \frac{F(x+h)-F(x)}{h} = \frac{1}{h}\left(\int_{a}^{x+h}f(t)\, \mathrm{d}t-\int_{a}^{x}f(t)\,\mathrm{d}t\right)\] \[ =\frac{1}{h}\int_{x}^{x+h}f(t)\,\mathrm{d}t = \frac{1}{h}f(c)(x+h-x) = f(c). \] As \(h\to0\) we see that \(c\to x\) and from the continuity of \(f\) it follows that \(f(c)\to f(x)\). Thus \(F'(x)=f(x)\).
\(\square\)
Antiderivative
If \(F'(x)=f(x)\) on some open interval then \(F\) is the antiderivative (or the primitive function) of \(f\). The fundamental theorem of calculus guarantees that for every continuous function \(f\) there exists an antiderivative \[ F(x) = \int_{a}^{x}f(t)\,dt. \] The antiderivative is not necessarily expressible as a combination of elementary functions even if \(f\) were an elementary function, e.g. \(f(x) = e^{-x^{2}}\). Such primitives are called nonelementary antiderivatives.
Theorem.
Antiderivatives are only unique up to a constant; \[\int f(x)\,dx = F(x) + C, C\in\mathbb{R} \text{ constant }\] if \(F'(x)=f(x)\).
Suppose that \(F'_{1}(x)=F'_{2}(x)=f(x)\) for all \(x\). Then the derivative of \(F_{1}(x)-F_{2}(x)\) is identically zero and thus the difference is a constant.
\(\square\)
(Second) Fundamental theorem of calculus
Let \(f\colon\left[a,b\right]\to\mathbb{R}\) be a continuous function and \(G\) an antiderivative of \(f\), then \[\int_{a}^{b}f(x)\,dx = G(x)\Big|_{x=a}^{x=b} = G(b)-G(a). \]
Because \(F(x)=\int_{a}^{x}f(t)\,dt\) is an antiderivative of \(f\) then due to continuity \(F(x)-G(x)=C=\text{constant}\) for all \(x\in\left[a,b\right]\). Substituting \(x=a\) we find that \(C=-G(x)\). Thus \[\int_{a}^{x}f(t)\,dt = F(x) = G(x)-G(a)\] and substituting \(x=b\) the result follows.
\(\square\)
Suppose that \(f\) is a continuous function and that \(a\) and \(b\) are differentiable functions. Then \[\frac{d}{dx}\int_{a(x)}^{b(x)}f(t)\,dt = f(b(x))b'(x)-f(a(x))a'(x).\]
Suppose that \(F\) is an antiderivative of \(f\). Then from the fundamental theorem of calculus and the chain rule it follows that \[\frac{d}{dx}\int_{a(x)}^{b(x)}f(t)\,dt = \frac{d}{dx}\big(F(b(x)) - F(a(x))\big)\] \[=\frac{d}{dx}F(b(x)) - \frac{d}{dx}F(a(x)) = F'(b(x))b'(x) - F'(a(x))a'(x) \] \[ = f(b(x))b'(x) - f(a(x))a'(x). \]
\(\square\)
Integrals of elementary functions
Constant Functions
Given the constant function \(f(x) = c,\,c\in\mathbb{R}\). The integral \(\int\limits_a^b f(x)\,\mathrm{d} x = \int\limits_a^b c \, \mathrm{d}x\) has to be determined now.
Solution by finding a antiderivative
From the previous chapter it is known that \(g(x) = c\cdot x\) gives \(g'(x) = c\). This means that \(c \cdot x\) is an antiderivative for \(c\). So the following applies \[\int\limits_a^b c \, \mathrm{d}x = [c \cdot x]_{x=a}^{x=b} = c\cdot b - c \cdot a = c \cdot (b-a).\]
Remark: Of course, a function \(h(x) = c \cdot x + d\) would also be an antiderivative of \(f\), since the constant \(d\) is omitted in the derivation. For sake of simplicity \(c \cdot x\) can be used, since \(d\) can be chosen as \(d=0\) for definite integrals.
Solution by geometry
The area under the constant function forms a rectangle with height \(c\) and length \(b-a\). Thus the area is \(c \cdot (b-a)\) and this corresponds to the solution of the integral. Illustrate this remark by a sketch.
Linear functions
Given is the linear function \( f(x) = mx\). We are looking for the integral \(\int\limits_a^b f(x)\, \mathrm dx=\int\limits_a^b mx\, \mathrm dx\).
Solve by finding a antiderivative
The antiderivative of a linear function is in any case a quadratic function, since \(\frac{\mathrm d x^2}{\mathrm dx} = 2x \). The derivative of a quadratic function results in a linear function. Here, it is important to consider the leading factor as in \[\frac{\mathrm d (m \cdot \frac{1}{2} \cdot x^2)}{\mathrm dx} = mx.\] Thus the result is \[\int\limits_a^b mx \mathrm{d}x = \left[\frac{m}{2}x^2 \right]_{x=a}^{x=b}= \frac{m}{2}b^2 - \frac{m}{2}a^2. \]
Solving by geometry
The integral \(\int\limits_a^b mx\, \mathrm dx\) can be seen geometrically, as subtracting the triangle with the edges \((0|0)\), \((a|0)\) and \((a| ma)\) from the triangle with the edges \((0|0)\), \((b|0)\) and \((b| mb)\). Since the area of a triangle ist given by \(\frac{1}{2} \cdot \mbox{baseline} \cdot \mbox{height}\), the area of the first triangle \(\frac{1}{2}\cdot b \cdot mb = \frac{1}{2}mb^2\) and that of the second triangle is analogous \(\frac{1}{2}ma^2\). For the integral the result is \(\frac{m}{2}b^2 - \frac{m}{2}a^2\). This is consistent with the integral calculated using the antiderivative. Illustrate this remark by a sketch.
Power functions
In constant and linear functions we have already seen that the exponent of a function decreases by one when it is derived. So it has to get bigger when integrating. The following applies: \[\frac{\mathrm d x^n}{\mathrm dx} = n \cdot x^{n-1}. \] It follows that the antiderivative for \(x^n\) must have the exponent \(n+1\), \[\frac{\mathrm d x^{n+1}}{\mathrm dx} = (n+1) \cdot x^n.\] By multiplying the last equation with \(\frac{1}{n+1}\) we get \[\frac{\mathrm d}{\mathrm dx}\frac{1}{n+1} x^{n+1} = \frac{n+1}{n+1} \cdot x^n = x^n.\] Finally the antiderivative is \(\int x^n\, \mathrm dx = \frac{1}{n+1} x ^{n+1}+c,\,c\in\mathbb{R}\).
Examples
- \(\int x^2\, \mathrm dx = \frac{1}{3} x^3 +c,\,c\in\mathbb{R}\)
- \(\int x^3\, \mathrm dx = \frac{1}{4} x^4 +c,\,c\in\mathbb{R}\)
- \(\int x^{20}\, \mathrm dx = \frac{1}{21} x^{21} +c,\,c\in\mathbb{R}\)
The formula \(\int x^n\, \mathrm dx = [\frac{1}{n+1} x^{n+1}] \) is also valid, if the exponent of the function is a real number and not equal \(-1\).
Examples
- \(\int x^{2,7}\, \mathrm dx = \frac{1}{3,7} x^{3,7}+c,\,c\in\mathbb{R}\)
- \(\int \sqrt{x}\, \mathrm dx = \int x^\frac{1}{2} = \frac{2}{3} x^{\frac{3}{2}}+c,\,c\in\mathbb{R}\)
- But: For \(x\gt0\) applies\(\int x^{-1}\,\mathrm d x=\ln(x)+c,\,c\in\mathbb{R}.\)
Natural Exponential function
The natural exponential function \(f(x) = e^x\) is one of the easiest function to differentiate and integrate. Since the derivation of \(e^x\) results in \(e^x\), it follows \[\int e^x\, \mathrm dx = e^x +c, \, c\in \mathbb{R}.\]
Example 1
Determine the value of the integral \(\int_0^1 e^z \,\mathrm{d} z\).
\[\int\limits_0^1e^z\,\mathrm{d}z= e^z\big|_{z=0}^{z=1}=e^1-e^0=e-1.\]
Example 2
Determine the value of the integral \(\int_0^b e^{\alpha t} \,\mathrm{d} t\). Using the same considerations as above we get \[\int\limits_0^b e^{\alpha t}\,\mathrm{d}t= \frac{1}{\alpha}e^{\alpha t}\big|_{t=0}^{t=b} =\frac{1}{\alpha}\left(e^{\alpha b}-e^0\right)=\frac{1}{\alpha}\left(e^{\alpha b}-1\right).\] Important is here, that we have to use the factor \(\frac1{\alpha}\).
Natural Logarithm
The derivative of the natural logarithmic function is \(\ln'(x) =\frac{1}{x}\) for \(x\gt0\). It even applies \(\ln'(x) =\frac{1}{x}\) to \(x<0\). These results together result in for the antiderivative of \(\frac{1}{x}\)
\[\int \frac{1}{x}\,\mathrm{d}x = \ln\left(|x|\right) +c , c\in\mathbb{R}.\]
An antiderivative can be specified for the natural logarithm: \[\int \ln(x)\,\mathrm{d}x = x\ln(x) - x + c ,\, c\in\mathbb{R}.\]
Trigonometric function
The antiderivatives of \(\sin(x)\) and \(\cos(x)\) also result logically if you derive "backwards". We have \[\int \sin(x)\, \mathrm dx = -\cos(x)+c,\,c\in\mathbb{R},\] since \( (-\cos(x))' =-(-\sin(x))=\sin(x).\) Furthermore we know \[\int \cos(x)\, \mathrm dx = \sin(x)+c,\,c\in\mathbb{R},\] since \((\sin(x))' = \cos(x) \) applies.
Example 1
Which area is covered by the sine on the interval \([0,\pi]\) and the \(x\)-axis? To determination the area we simply have to evaluate the integral \[\int_0^{\pi} \sin(\tau) \, \mathrm{\tau}.\] That means \[\int_0^{\pi} \sin(\tau) \, \mathrm{d}\tau = \left[-\cos(\tau)\right]_{\tau=0}^{\tau=\pi} = -\cos(\pi) - (-\cos(0)) = -(-1) - (-1) = 2.\] Again make a sketch for this example.
Example 2
How can the integral \(\int \cos(\omega t +\phi)\,\mathrm{d}t\) be expressed analytically?
To determine the integral we use the antiderivative of the cosine: \(\sin'(x) = \cos(x)\). However, the inner derivativ has to be considered in the given function and thus we get \[\int \ \cos(\omega t +\phi)\,\mathrm{d}t =\frac{1}{\omega}\sin(\omega t+\phi)+c,\,c\in\mathbb{R}.\]
Summary:
The most common antiderivatives follow from the rules of differentiation: \[\int x^{r}\,dx = \frac{1}{r+1}x^{r+1} + C, ~r\neq-1\] \[\int x^{-1}\,dx = \ln|x| + C\] \[\int e^{x}\,dx = e^{x} + C\] \[\int \sin x\,dx = -\cos x + C\] \[\int \cos x\,dx = \sin x + C\] \[\int \frac{dx}{1+x^{2}} = \arctan x + C\]
Example 1
Evaluate the integrals \(\displaystyle \int_{-1}^{1}e^{-x}\,dx\) and \(\displaystyle\int_{0}^{1}\sin(\pi x)\,dx\).
Solution. The antiderivative of \(e^{-x}\) is \(-e^{-x}\) so we have that \[\int_{-1}^{1}e^{-x}\,dx = -e^{-1}+e^{1} = 2\sinh1.\] The antiderivative of \(\sin(\pi x)\) is \(-\frac{1}{\pi}\cos(\pi x)\) and thus \[\int_{0}^{1}\sin(\pi x)\,dx = -\frac{1}{\pi}(\cos\pi-\cos0) = \frac{2}{\pi}.\]
Example 2
Evaluate the integral \(\displaystyle\int_{0}^{1}\frac{x}{\sqrt{25-9x^{2}}}\,dx\).
Solution. The antiderivative might look something like \(F(x)=a(25-9x^{2})^{1/2}\), where we can find the factor \(a\) through differentiation: \[D\big(a(25-9^{2})^{1/2}\big) = a\cdot\frac{1}{2}\cdot(-18x)(25-9x^{2})^{-1/2} = \frac{-9ax}{\sqrt{25-9x^{2}}}\] hence if \(a=-1/9\) we get the correct antiderivative. Thus \[\int_{0}^{1}\frac{x}{\sqrt{25-9x^{2}}}\,dx = -\frac{1}{9}\cdot(25-9x^{2})^{1/2}\Big|_{x=0}^{x=1} = -\frac{1}{9}(\sqrt{16}-\sqrt{25}) = \frac{1}{9}.\] This integral can also be solved using integration by substitution; more on this method later.
Geometric applications
Area of a plane region
Suppose that \(f\) and \(g\) are piecewise continuous functions. The area of a region bounded by the graphs \(y=f(x)\), \(y=g(x)\) and the vertical lines \(x=a\) and \(x=b\) is given by the integral \[A=\int_{a}^{b}|f(x)-g(x)|\,dx.\]
Especially if \(f\) is a non-negative function on the interval \([a,b]\) and \(g(x)=0\) for all \(x\) then the integral \[A=\int_{a}^{b}f(x)\,dx\] is the area of the region bounded by the graph \(y=f(x)\), the \(x\)-axis and the vertical lines \(x=a\) and \(x=b\).
Arc length
The arc length \(\ell\) of a planar curve \(y=f(x)\) between points \(x=a\) and \(x=b\) is given by the integral \[\ell = \int_{a}^{b}\sqrt{1+f'(x)^{2}}\,dx.\]
Heuristic reasoning: On a small interval \(\left[x,x+\Delta x\right]\) the arc length of the curve between \(y=f(x)\) and \(y=f(x+\Delta x)\) is approximately \[\Delta s \approx \sqrt{\Delta x^{2} + \Delta y^{2}} = \Delta x\sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^{2}} \approx \Delta x\sqrt{1+f'(x)^{2}}.\]
Surface of revolution
The area of a surface generated by rotating the graph \(y=f(x)\) around the \(x\)-axis on the interval \(\left[a,b\right]\) is given by \[A = 2\pi\int_{a}^{b}|f(x)|\sqrt{1+f'(x)^{2}}\,dx.\] Heuristic reasoning: An area element of the surface is approximately \[\Delta A \approx \text{perimeter}\cdot\text{length} = 2\pi|f(x)|\cdot\Delta s.\]
Solid of revolution
Suppose that the cross-sectional area of a solid is given by the function \(A(x)\) when \(x\in\left[a,b\right]\). Then the volume of the solid is given by the integral \[V = \int_{a}^{b}A(x)\,dx.\] If the graph \(y=f(x)\) is rotated around the \(x\)-axis between the lines \(x=a\) and \(x=b\) the volume of the generated figure (the solid of revolution) is \[V = \pi\int_{a}^{b}f(x)^{2}\,dx.\] This follows from the fact that the cross-sectional area of the figure at \(x\) is a circle with radius \(f(x)\) i.e. \(A(x)=\pi f(x)^{2}\).
More generally: Let \(0\le g(x)\le f(x)\) and suppose that the region bounded by \(y=f(x)\) and \(y=g(x)\) and the lines \(x=a\) and \(x=b\) is rotated around the \(x\)-axis. The volume of this solid of revolution is \[V = \pi\int_{a}^{b}\big(f(x)^{2}-g(x)^{2}\big)\,dx.\]
Improper integral
Definition: Improper integral
- 1st kind: The integral is defined on an unbounded domain, \(\left[a,\infty\right[,\left]-\infty,b\right]\) or the entire \(\mathbb{R}\).
- 2nd kind: The integrand function is unbounded in the domain of integration or a two-sided limit doesn't exist on one or both of the endpoints of the integral
One limitation of the improper integration is that the limit must be taken with respect to one endpoint at a time.
Example
\[\int_{0}^{\infty}\frac{dx}{\sqrt{x}(1+x)} = \int_{0}^{1}\frac{dx}{\sqrt{x}(1+x)} + \int_{1}^{\infty}\frac{dx}{\sqrt{x}(1+x)}\] Provided that both of the integrals on the right-hand side converge. If either of the two is divergent then so is the integral.
Definition
Let \(f\colon\left[a,\infty\right[\to\mathbb{R}\) be a piecewise continuous function. Then \[\int_{a}^{\infty}f(x)\,dx = \lim_{R\to\infty}\int_{a}^{R}f(x)\,dx\] provided that the limit exists and is finite. We say that the improper integral of \(f\) converges over \(\left[a,\infty\right[\).
Likewise for \(f\colon\left]-\infty,b\right]\to\mathbb{R}\) we define \[\int_{-\infty}^{b}f(x)\,dx = \lim_{R\to\infty}\int_{-R}^{b}f(x)\,dx\] provided that the limit exists and is finite.
Example
Find the value of \(\displaystyle\int_{0}^{\infty}e^{-x}\,dx\).
Solution. Notice that \[\int_{0}^{R}e^{-x}\,dx = \left(-e^{-x}\right)\Bigg|_{x=0}^{R}=1-e^{-R}\to 1\] as \(R\to\infty\). Thus the improper integral converges and \[\int_{0}^{\infty}e^{-x}\,dx = 1.\]
Definition
Let \(f\colon\mathbb{R}\to\mathbb{R}\) be a piecewise continuous function. Then \[\int_{-\infty}^{\infty}f(x)\,dx = \int_{-\infty}^{0}f(x)\,dx + \int_{0}^{\infty}f(x)\,dx\] if both of the two integrals on the right-hand side converge.
In the case \(f(x)\ge0\) for all \(x\in\mathbb{R}\) the following holds \[\int_{-\infty}^{\infty}f(x)\,dx = \lim_{R\to\infty}\int_{-R}^{R}f(x)\,dx.\]
However, this doesn't apply in general. For example, let \(f(x)=x\). Note that even though \[ \int_{-R}^{R}f(x)\,dx = \int_{-R}^{R}x\,dx = \frac{R^2}{2} - \frac{(-R)^2}{2} = 0 \] for all \(R\in\mathbb{R}\) the improper integral \[ \int_{-\infty}^{\infty}x\,dx = \lim_{R\to\infty}\int_{-R}^{0}x\,dx + \lim_{R\to\infty}\int_{0}^{R}x\,dx = \lim_{R\to\infty}-\frac{(-R)^2}{2} + \lim_{R\to\infty}\frac{R^2}{2} = \infty - \infty \] does not converge.
Improper integrals of the 2nd kind are handled in a similar way using limits. As there are many different (but essentially rather similar) cases, we leave the matter to one example only.
Example
Find the value of the improper integral \(\displaystyle\int_{0}^{1}\frac{dx}{\sqrt{x}}\).
Solution. We get \[\int_{\epsilon}^{1}\frac{dx}{\sqrt{x}} = \left(2\sqrt{x}\right)\Bigg|_{x=\epsilon}^{x=1} = 2-2\sqrt{\epsilon} \to 2,\] as \(\epsilon\to0+\). Thus the integral converges and its value is \(2\).
Comparison test
Theorem.
Suppose that \(f\) and \(g\) are integrable functions such that \(|f(x)|\le g(x)\) for \(a < x < b\).- If the improper integral \[I=\int_{a}^{b}g(x)\,dx\] converges then so does \(\displaystyle\int_{a}^{b}f(x)\,dx\) and its value is less than or equal to \(I\).
- If the improper integral \[\int_{a}^{b}f(x)\,dx\] diverges then so does \(\displaystyle\int_{a}^{b}g(x)\,dx\).
Example 2
Notice that \[0\le\frac{1}{\sqrt{x}(1+x)}\le\frac{1}{\sqrt{x}}, \text{ for }0 < x < 1\] and that the integral \[\int_{0}^{1}\frac{dx}{\sqrt{x}} = 2\] converges. Thus by the comparison test the integral \[\int_{0}^{1}\frac{dx}{\sqrt{x}(1+x)}\] also converges and its value is less than or equal to \(2\).
Example 3
Likewise \[0\le\frac{1}{\sqrt{x}(1+x)} < \frac{1}{\sqrt{x}(0+x)}=\frac{1}{x^{3/2}}, \text{ for }x\ge1\] and because \(\displaystyle\int_{1}^{\infty}x^{3/2}\,dx=2\) converges so does \[\int_{1}^{\infty}\frac{dx}{\sqrt{x}(1+x)}\] and its value is less than or equal to \(2\).
Note. The choice of the dominating function depends on both the original function and the interval of integration.
Example 4
Determine whether the integral \[\int_{0}^{\infty}\frac{x^2+1}{x^3(\cos^2{x}+1)}\,dx\] converges or diverges.
Solution. Notice that \(x^2+1\ge x^2\) for all \(x\in\mathbb{R}\) and therefore \[\frac{x^2+1}{x^3(\cos^2{x}+1)} \ge \frac{1}{x\underbrace{(\cos^2{x}+1)}_{\le 2}} \ge \frac{1}{2x}.\] Now, because the integral \(\displaystyle\int_{0}^{\infty}\frac{dx}{2x}\) diverges then by the comparison test so does the original integral.
Integration techniques
Logarithmic integration
Given a quotient of differentiable functions, we know to apply the quotient rule. However, this is not so easy with integration. Here only for a few special cases we will state rules in this chapter.
Logarithmic integration As we already know the derivative of \(\ln(x)\), i.e. the natural logarithm to the base \(e\), equal to \(\frac{1}{x}\). According to the chain rule the derivative of differentiable function with positive function values is \(f\,:\,\frac{\mathrm d}{\mathrm dx} \ln (f(x)) = \frac{f'(x)}{f(x)}\). This means that for a quotient of functions where the numerator is the derivative of the denominator yields the rule: \begin{equation} \int \frac{f'(x)}{f(x)}\, \mathrm{d} x= \ln \left(|f(x)|\right) +c,\,c\in\mathbb{R}.\end{equation} Using the absolute value of the function is important, since the logarithm is defined on \(\mathbb{R}^+\).
Examples
- \(\int \frac{1}{x}\, \mathrm dx = \int \frac{x'}{x} \mathrm\, dx = \ln(|x|) +c,\,c\in\mathbb{R} \).
- \(\int \frac{3x^2 + 17}{x^3 +17x - 15}\, \mathrm dx = \ln(|x^3 + 17x - 15|)+c,\,c\in\mathbb{R}\).
- \(\int \frac{\cos(x)}{\sin(x)}\,\mathrm dx = \ln(|\sin(x)|)+c,\,c\in\mathbb{R}\).
Integration of rational functions - partial fraction decomposition
The logarithmic integration works well in special cases of broken rational functions where the counter is a multiple of the derivation of the denominator. However, other cases can sometimes be traced back to this. This method is called partial fractional decomposition, which represents rational functions as the sum of proper rational functions.
Example 1
The function \(\frac{1}{1-x^2}\) cannot be integrated at first glance. However, the denominator \(1-x^2\) can be written as \((1-x)(1+x)\) and the function can finally reads as \(\dfrac{1}{1-x^2} = \dfrac{\frac{1}{2}}{1+x} + \dfrac{\frac{1}{2}}{1-x}\) by partial fraction decomposition. This expression can be integrated, as demonstrated now: \begin{eqnarray} \int \dfrac{1}{1-x^2} \,\mathrm dx &= & \int \dfrac{\frac{1}{2}}{1+x} + \dfrac{\frac{1}{2}}{1-x}\, \mathrm dx \\ & =& \frac{1}{2} \int \dfrac{1}{1+x}\, \mathrm dx - \frac{1}{2} \int \dfrac{-1}{1-x}\, \mathrm dx\\ & = &\frac{1}{2} \ln|1+x| +c_1 - \frac{1}{2} \ln|1-x| +c_2\\ &= &\frac{1}{2} \ln \left|\dfrac{1+x}{1-x}\right|+c,\,c\in\mathbb{R}. \end{eqnarray} This procedure is now described in more detail for some special cases.
Case 1: \(Q(x)=(x-\lambda_1)(x-\lambda_2)\) with \(\lambda_1\ne\lambda_2\). In this case, \(R\) has the representation \(R(x) = \frac{ax+b}{(x-\lambda_1)(x-\lambda_2)}\) and can be transformed to \[\frac{ax+b}{(x-\lambda_1)(x-\lambda_2)} = \frac{A}{(x-\lambda_1)}+\frac{B}{(x-\lambda_2)}.\] By multiplying with \((x-\lambda_1)(x-\lambda_2)\) it yields ot \[ax+b = A(x-\lambda_1) + B(x-\lambda_2) = \underbrace{(A+B)}_{\stackrel{!}{=}a}x + \underbrace{(-A\lambda_1-B\lambda_2)}_{\stackrel{!}{=}b}.\]
\(A\) and \(B\) are now obtained by the method of equating the coefficients.
Example 2
Determe the partial fraction decomposition of \(\frac{2x+3}{(x-4)(x+5)}\).
Start with the equation \[\frac{2x+3}{(x-4)(x+5)} = \frac{A}{(x-4)}+\frac{B}{(x+5)}\] to get the parameters \(A\) and \(B\). Multiplication by \({(x-4)(x+5)}\) leads to \[2x+3 = A(x+5)+B(x-4) = (A+B)x +5A -4B.\] Now we get the system of linear equations
\begin{eqnarray}A+B & = & 2 \\ 5A - 4 B &=& 3\end{eqnarray} with the solution \(A = \frac{11}{9}\) and \(B= \frac{7}{9}\). The representation with proper rational functions is \[\frac{2x+3}{(x-4)(x+5)}=\frac{11}{9}\frac{1}{(x-4)}+\frac{7}{9}\frac{1}{(x+5)} \] The integral of the type \(\int \frac{ax+b}{(x-\lambda_1)(x-\lambda_2)}\,\mathrm{d} x.\) is no longer mystic.
With the help of partial fraction decomposition, this integral can now be calculated in the following manner \begin{eqnarray}\int \frac{ax+b}{(x-\lambda_1)(x-\lambda_2)}\mathrm{d} x &=& \int\frac{A}{(x-\lambda_1)}+\frac{B}{(x-\lambda_2)}\mathrm{d} x \\ &=&A\int\frac{1}{(x-\lambda_1)}\mathrm{d} x +B\int\frac{1}{(x-\lambda_2)}\mathrm{d} x \\ & = & A\ln(|x-\lambda_1|) + B\ln(|x-\lambda_2|).\end{eqnarray}
Example 3
Determine the antiderivative for \(\frac{2x+3}{(x-4)(x+5)}\), i.e. \(\int\frac{2x+3}{(x-4)(x+5)}\,\mathrm{d} x.\)
From the above example we already know: \[\int\frac{2x+3}{(x-4)(x+5)}\,\mathrm{d} x = \int\frac{11}{9}\frac{1}{(x-4)}+\frac{7}{9}\frac{1}{(x+5)}\, \mathrm{d} x.\]
Using the idea explained above immediately follow: \[\int\frac{11}{9}\frac{1}{(x-4)}+\frac{7}{9}\frac{1}{(x+5)} \,\mathrm{d} x = \frac{11}{9}\int\frac{1}{(x-4)} \mathrm{d} x + \frac{7}{9}\int\frac{1}{(x+5)} \,\mathrm{d} x= \frac{11}{9}\ln(|(x-4)|)+\frac{7}{9}\ln(|(x+5)|).\] So is the result \[\int\frac{2x+3}{(x-4)(x+5)}\,\mathrm{d} x=\frac{11}{9}\ln(|(x-4)|)+\frac{7}{9}\ln(|(x+5)|).\]
Case 2: \(Q(x)=(x-\lambda)^2\).
In this case \(R\) has the representation \(R(x) = \frac{ax+b}{(x-\lambda)^2}\) and the ansatz \[\frac{ax+b}{(x-\lambda)^2} = \frac{A}{(x-\lambda)}+\frac{B}{(x-\lambda)^2}\] is used.
By multiplying the equation with \((x-\lambda)^2\) we get \[ax+b = A(x-\lambda) + B.\] Again equating the coefficients leads us to a system of linear equations in \(A=a\) and \(B=b+A\lambda=b+a\lambda.\)
So we have \[\int \frac{ax+b}{(x-\lambda)^2}\,\mathrm{d}x = \int \frac{a}{(x-\lambda)}+\frac{b+a\lambda}{(x-\lambda)^2} \mathrm{d}x =a\ln(|x-\lambda|)-\frac{b+a\lambda}{(x-\lambda)}+c,\,c\in\mathbb{R}. \]
3. case \(Q(x)=x^2+mx+n\) without real zeros.
In this case \(R\) has the representation \(R(x) = \frac{ax+b}{x^2+mx+n}\) and the representation can not be simplified.
Only the special case \(R(x) = \frac{2x+m}{x^2+mx+n}\) is now considered.
In this case we have \[\int \frac{2x+m}{x^2+mx+n}\,\mathrm{d}x = \ln(|x^2+mx+n|)+c, \quad c\in\mathbb{R}. \]
Another special case is \(R(x) = \frac{1}{x^2+1}\) with \[\int \frac{1}{x^2+1} \, \mathrm{d} x = \arctan(x) +c,\quad c\in \mathbb{R}.\]
Integration by Parts
The derivative of a product of two continuously differentiable functions \(f\) and \(g\) is \[(f(x)\cdot g(x))' = f'(x)\cdot g(x)+f(x)\cdot g'(x),\quad x\in(a,b).\]
This leads us to the following theorem:
Theorem: Integration by Parts
Let\(f\) and \(g\) be continuously differentiable functions on the interval \(\left[a,b\right]\). Then \[\int_{a}^{b}f'(x)g(x)\,dx = f(b)g(b)-f(a)g(a)-\int_{a}^{b}f(x)g'(x)\,dx\] Likewise for the indefinite integral it holds that \[\int f'(x)g(x)\,dx = f(x)g(x)-\int f(x)g'(x)\,dx.\]
It follows from the product rule that \[\frac{d}{dx}(f(x)g(x)) = f'(x)g(x) + f(x)g'(x)\] or rearranging the terms \[f'(x)g(x) = \frac{d}{dx}(f(x)g(x)) - f(x)g'(x). \] Integrating both sides of the equation with respect to \(x\) and ignoring the constant of integration now yields \[\int f'(x)g(x) = f(x)g(x) - \int f(x)g'(x)\,dx.\]
Example
Solve the integral \(\displaystyle\int_{0}^{\pi}x\sin x\,dx\).
Solution. Set \(f'(x)=\sin x\) and \(g(x) = x\). Then \(f(x)=-\cos x\) and \(g'(x) = 1\) and the integration by parts gives \[\int_{0}^{\pi}x\sin x\,dx = -\pi\cos\pi - 0 - \int_{0}^{\pi}(-\cos x)\,dx\] \[=\pi+\left(\sin x\right)\Bigg|_{x=0}^{\pi} = \pi.\]
Notice that had we chosen \(f\) and \(g\) the other way around this would have led to an even more complicated integral.
Integration by Substitution
Theorem: Integration by substitution
Let \(f\) and \(g\) be continuously differentiable functions on \(\left[a,b\right]\). Then \[\int_{a}^{b}f(g(x))g'(x)\,dx = \int_{g(a)}^{g(b)}f(u)\,du.\]
Let \(F'(x)=f(x)\). Then \[\int_{a}^{b}f(g(x))g'(x)\,dx = \int_{a}^{b}(F\circ g)'(x)\,dx\] \[= (F\circ g)(b) - (F\circ g)(a) = F(g(b)) - F(g(a))\] \[= \int_{g(a)}^{g(b)}f(u)\,du.\]
In practise: Substituting \(u=g(x)\) we have (heuristically) \[\frac{du}{dx}=g'(x)\Rightarrow du=g'(x)\,dx\] and the limits of integration \(x=a\Rightarrow u=g(a),x=b\Rightarrow u=g(b)\).
Example 1
Find the value of the integral \(\displaystyle\int_{0}^{\pi^2}\sin\sqrt{x}\,dx\).
Solution. Making the substitution \(x=t^{2}\) when \(t\ge0\) we have \(dx=2t\,dt\). Solving the limits from the inverse formula i.e. \(t=\sqrt{x}\) we find that \(t(0)=0\) and \(t(\pi^{2})=\pi\). Hence \[\int_{0}^{\pi^{2}}\sin\sqrt{x}\,dx = \int_{0}^{\pi^{2}}2t\sin t\,dt = 2\int_{0}^{\pi}t\sin t\,dt = 2\pi.\]
Here the latter integral was solved applying integration by parts in the previous example.
Example 2
Find the antiderivative of \(\displaystyle\frac{1}{\sqrt{x}(1+x)}\).
Solution. Substituting \(x=t^{2}\), \(t>0\) or \(t=\sqrt{x}\) gives \[\int\frac{dx}{\sqrt{x}(1+x)} = \int\frac{2t}{t(1+t^{2})}\,dt = 2\arctan t + C = 2\arctan\sqrt{x} + C.\]
9. Differential equations
Introduction
Differential equation is an equation containing an unknown function, e.g. \( y = y(x) \), and its derivatives \( y'(x), y''(x), \ldots, y^{(n)}(x) \). This kind of equation where the unknown function depends on a single variable, is called an ordinary differential equation (ODE) or simply a differential equation. If the unknown function contains several variables, it is called partial differential equation, but they are not covered in this course.
A typical application leading to a differential equation is radioactive decay. If \( y=y(t) \) is the number of radioactive nuclei present at time \( t \), then during a short time interval \( \Delta t\) the
change in this number is approximately \( \Delta y \approx -k y(t)\cdot \Delta t\), where \( k\) is a positive constant depending on the radioactive substance. The approximation becomes better as \( \Delta t \to 0\), so that \( y'(t) \approx \Delta y/\Delta t \approx -ky(t) \). It follows that the differential equation \( y'(t)=-ky(t)\) is a mathematical model for the radioactive decay. In reality, the number of nuclei is an integer, so the function \( y(t)\) is not differentiable (or the derivative is mostly zero!). Therefore, the model describes the properties of some idealized smooth version of \( y(t)\). This is a typical phenomenon in most models.
Order
The order of a differential equation is the highest order of the derivatives appearing in the equation.
For example, the order of the differential equation \( y' + 3y = \sin(x)\) is 1. The order of the differential equation \( y'' + 5y' -6y = e^x \) is 2.
Here the variable of the function \(y\) is not visible; the equation is considered to determine \(y\) implicitly.
Solutions of a differential equation
A differential equation of order n is of the form
\( \begin{equation} \label{dydef}
F(x, y(x), y'(x),\ldots , y^{(n)}(x)) = 0
\end{equation} \)
The solution to an ODE is an n times differentiable function \(y(x)\) satisfying the above equation for all \( x \in I, \) where \(I\) is an open interval in the real axis.
Typically the solution is not unique and there can be an infinite number of solutions. Consider the equation \( xy^2 + y' = 0. \) The equation has the solutions
- \( y_0(x) = 0,\enspace x \in \mathbb{R} \)
- \( y_1(x) = 2/x^2,\enspace x>0 \)
- \( y_2(x) = 2/x^2,\enspace x<0 \)
- \( y_3(x) = 2/(x^2 + 3),\enspace x \in \mathbb{R} \)
Here \( y_1\), \( y_2\) and \( y_3 \) are called particular solutions. The general solution is \( y(x) = 2/(x^2 + C),\> C \in \mathbb{R}. \) Particular solutions can be derived from the general solution by assigning the parameter \(c\) to some value. Solutions that cannot be derived from the general solution are called special solutions.
Differential equations do not necessarily have any solutions at all. For example, the first order differential equation \( \sin(y' + y) = 2 \) does not have any solutions. If a first order equation can be written in normal form \( y' = f(x,y) \), where \(f\) is continuous, then a solution exists.
Initial condition
Constants in the general solution can be assigned to some values if the solution is required to satisfy additional properties. We may for example demand that the solution equals \( y_0 \) at \( x_0 \) by setting an initial condition \( y(x_0) = y_0. \) With first order equations, only one condition is (usually) needed to make the solution unique. With second order equations, we need two conditions, respectively. In this case, the initial condition is of the form
\( \left\{ \begin{array}
yy(x_0) = y_0 \\ y'(x_0) = y_1 \end{array} \right. \)
In general, for an equation of order n, we need n extra conditions to make the solution unique. A differential equation and its set initial conditions are jointly referred as an initial value problem.
Example 1.
We saw above that the the general solution to the differential equation \( xy^2 + y' = 0 \) is \( y(x) = 2/(x^2 + C).\) Therefore the solution to the initial value problem
\( \left\{\begin{align} xy^2 + y' = 0 \\ y(0) = 1 \end{align} \right. \)
is \( y(x) = 2/(x^2 + 2).\)
Interactive. In the figure above, some of the solutions to the equation
Direction field
The differential equation \( y' = f(x,y) \) can be interpreted geometrically: if the solution curve (i.e. graph of a solution) goes through the point \( (x_0, y_0) \), then it holds that \( y'(x_0) = f(x_0, y_0) \), i.e. we can find the slopes of the tangents of the curve even if we do not know the solution itself. Direction field or slope field is a vector field \( \vec{i} + f(x_k, y_k)\vec{j} \) drawn through the points \( (x_k, y_k)\). The direction field provides a fairly accurate image of the behavior of the solution curves.
Interactive. In the picture above we have drawn the direction field corresponding to the differential equation \( y' = \sin(xy) \). As shown here, an initial value often determines the solution also in the negative direction.
1st Order Ordinary Differential Equations
A manifesting problem in the theory of differential equations is that there is only a relatively small amount of methods for finding solutions that are generally applicable. Even for a fairly simple differential equation a generalized formula does not usually exist, and especially for higher order differential equations it is rare to be able to find an analytic solution. For some equations it is possible, however, and here some of the most common cases are introduced.
Linear 1st order ODE
If a differential equation is of the form
\( p_n(x)y^{(n)} + p_{n-1}(x)y^{(n-1)} + \cdots + p_1(x)y' + p_0(x)y = r(x),\)
then it is called a linear differential equation. The left side of the equation is a linear combination of the derivatives with multipliers \( p_k(x) \). Thus a first order linear ODE is of the form
\( p_1(x)y' + p_0(x)y = r(x). \)
If \( r(x) = 0 \) for all \(x\), then the equation is called homogeneous. Otherwise the equation is nonhomogeneous.
Theorem 1.
Consider a normal form initial value problem
\( \left\{\begin{align}y^{(n)} + p_{n-1}(x)y^{(n-1)} + \cdots + p_1(x)y' + p_0(x)y = r(x) \\ y(x_0) = y_0, \: y'(x_0) = y_1, \: \ldots, \: y^{n-1}(x_0) = y_{n-1}. \end{align} \right. \)
If the functions \( p_k\) and \( r\) are continuous in the interval \( (a,b)\) containing the initial point \(x_0\), then the initial value problem has a unique solution.
The condition concerning the normality of the equation is crucial. For example, the equation \(x^2y'' - 4xy' + 6y = 0 \) may have either zero or an infinite number of solutions depending on the initial condition: substituting \( x=0 \) to the equation automatically forces the initial condition \( y(0)=0\).
Solving a 1st order linear ODE
A first order linear ODE can be solved by using an integrating factor method. The idea of the method is to multiply both sides of the equation
\(y' + p(x)y = r(x) \) by the integrating factor \(\displaystyle e^{\int p(x) dx} =e^{P(x)}\), which allows the equation to be written in the form
\(\displaystyle y'(x)e^{P(x)} + p(x)e^{P(x)}y(x) = r(x)e^{P(x)} \Leftrightarrow \frac{d}{dx}\left( y(x)e^{P(x)}\right) = r(x)e^{P(x)}. \)
Integrating both sides of the equation, we get
\(\displaystyle y(x)e^{P(x)} = \int r(x)e^{P(x)}\, \mathrm{d}x + C
\Leftrightarrow y(x)= Ce^{-P(x)} + e^{-P(x)}\int r(x) e^{P(x)}\, \mathrm{d}x. \)
It is not advisable to try to remember the formula as it is, but rather keep in mind the
idea of how the equation should be modified in order to proceed.
Example 1.
Let us solve the differential equation \(\displaystyle y'-y = e^x+1.\) The integrating factor is \(\displaystyle e^{\int (-1)\, \mathrm{d}x} = e^{-x}\) so we multiply both sides by this expression:
\(\displaystyle e^{-x}y'-e^{-x}y = 1+e^{-x}\)
\(\displaystyle \frac{d}{dx}(y(x)e^{-x}) = 1+e^{-x}\)
\(\displaystyle y(x)e^{-x} = \int 1+e^{-x}\, \mathrm{d}x + C = x - e^{-x} + C\)
\(\displaystyle y(x)= e^xx - 1 + Ce^x.\)
Example 2.
Let us solve the initial value problem
\( \left\{\begin{align}xy' = x^2 + 3y \\ y(0) = 1 \end{align} \right. \)
First, we want to express the problem in normal form:
\( \displaystyle y' - \frac{3}{x}y = x. \)
Now the integrating factor is \(\displaystyle e^{ \int \frac{3}{x} dx } =\displaystyle e^{ -3 \ln \vert x \vert } =\displaystyle e^{ \ln x^{-3} } =\displaystyle \frac{1}{x^3},\> x>0. \) Hence, we get
\(\displaystyle \frac{y'}{x^3} - \frac{3}{x^4}y = \frac{1}{x^2} \)
\(\displaystyle \frac{d}{dx}(\frac{y}{x^3}) = \frac{1}{x^2} \)
\(\displaystyle \frac{y}{x^3} = \int \frac{1}{x^2}\,
\mathrm{d}x + C = - \frac{1}{x} + C\)
\(y = Cx^3 - x^2 \)
We have found the general solution. Because
\(y(0) = C\cdot 0 - 0 = 0,\) that is, the value of the function does not equal the given initial value, the problem does not have a solution.
The main reason for this is that the initial condition is given at \( x_0=0\), where the normal form of the equation is not defined. Any other choice for \( x_0\) will lead to a
unique solution.
Example 3.
Let us solve the ODE \(xy'-2y=2\) given the initial conditions
- \(y(1)=0\)
- \(y(0)=0\).
From the form \(y'-(2/x)y=2/x\) we see that the equation in question is a linear ODE. The integrating factor is
\[
e^{-\int (2/x)\, \mathrm{d}x} = e^{-2\ln |x|} = e^{\ln (1/x^2)} = \frac{1}{x^2}.
\]
Multiplying by the integrating factor, we get
\[
(1/x^2)y'(x)-(2/x^3)y(x) =\frac{2}{x^3}
\Leftrightarrow
\frac{d}{dx}\left( \frac{y(x)}{x^2}\right) = \frac{2}{x^3},
\]
so the general solution to the ODE is \(y(x)=x^2 (-1/x^2+C)=Cx^2-1\). From the initial value \(y(1)=0\) it follows that
\(C=1\), but the other condition \(y(0)=0\) leads to a contradiction \(-1=0\).
Therefore, the solution in the (a) part is \(y(x)=x^2-1\), but a solution satisfying the initial condition of part b) does not exist: by substituting \( x=0 \),
the equation forces \( y(0)=-1\).
A first order linear ODE can be solved by using an integrating factor method. The idea of the method is to multiply both sides of the equation \(y' + p(x)y = r(x) \) by the integrating factor \(\displaystyle e^{\int p(x) dx} =e^{P(x)}\), which allows the equation to be written in the form
\(\displaystyle y'(x)e^{P(x)} + p(x)e^{P(x)}y(x) = r(x)e^{P(x)} \Leftrightarrow \frac{d}{dx}\left( y(x)e^{P(x)}\right) = r(x)e^{P(x)}. \)
Integrating both sides of the equation, we get
\(\displaystyle y(x)e^{P(x)} = \int r(x)e^{P(x)}\, \mathrm{d}x + C \Leftrightarrow y(x)= Ce^{-P(x)} + e^{-P(x)}\int r(x) e^{P(x)}\, \mathrm{d}x. \)
It is not advisable to try to remember the formula as it is, but rather keep in mind the idea of how the equation should be modified in order to proceed.
Example 1.
Let us solve the differential equation \(\displaystyle y'-y = e^x+1.\) The integrating factor is \(\displaystyle e^{\int (-1)\, \mathrm{d}x} = e^{-x}\) so we multiply both sides by this expression:
\(\displaystyle e^{-x}y'-e^{-x}y = 1+e^{-x}\)
\(\displaystyle \frac{d}{dx}(y(x)e^{-x}) = 1+e^{-x}\)
\(\displaystyle y(x)e^{-x} = \int 1+e^{-x}\, \mathrm{d}x + C = x - e^{-x} + C\)
\(\displaystyle y(x)= e^xx - 1 + Ce^x.\)
Example 2.
Let us solve the initial value problem
\( \left\{\begin{align}xy' = x^2 + 3y \\ y(0) = 1 \end{align} \right. \)
First, we want to express the problem in normal form:
\( \displaystyle y' - \frac{3}{x}y = x. \)
Now the integrating factor is \(\displaystyle e^{ \int \frac{3}{x} dx } =\displaystyle e^{ -3 \ln \vert x \vert } =\displaystyle e^{ \ln x^{-3} } =\displaystyle \frac{1}{x^3},\> x>0. \) Hence, we get
\(\displaystyle \frac{y'}{x^3} - \frac{3}{x^4}y = \frac{1}{x^2} \)
\(\displaystyle \frac{d}{dx}(\frac{y}{x^3}) = \frac{1}{x^2} \)
\(\displaystyle \frac{y}{x^3} = \int \frac{1}{x^2}\, \mathrm{d}x + C = - \frac{1}{x} + C\)
\(y = Cx^3 - x^2 \)
We have found the general solution. Because \(y(0) = C\cdot 0 - 0 = 0,\) that is, the value of the function does not equal the given initial value, the problem does not have a solution. The main reason for this is that the initial condition is given at \( x_0=0\), where the normal form of the equation is not defined. Any other choice for \( x_0\) will lead to a unique solution.
Example 3.
Let us solve the ODE \(xy'-2y=2\) given the initial conditions
- \(y(1)=0\)
- \(y(0)=0\).
From the form \(y'-(2/x)y=2/x\) we see that the equation in question is a linear ODE. The integrating factor is
\[ e^{-\int (2/x)\, \mathrm{d}x} = e^{-2\ln |x|} = e^{\ln (1/x^2)} = \frac{1}{x^2}. \]Multiplying by the integrating factor, we get
\[ (1/x^2)y'(x)-(2/x^3)y(x) =\frac{2}{x^3} \Leftrightarrow \frac{d}{dx}\left( \frac{y(x)}{x^2}\right) = \frac{2}{x^3}, \]so the general solution to the ODE is \(y(x)=x^2 (-1/x^2+C)=Cx^2-1\). From the initial value \(y(1)=0\) it follows that \(C=1\), but the other condition \(y(0)=0\) leads to a contradiction \(-1=0\). Therefore, the solution in the (a) part is \(y(x)=x^2-1\), but a solution satisfying the initial condition of part b) does not exist: by substituting \( x=0 \), the equation forces \( y(0)=-1\).
Separable equation
A first order differential equation is separable, if it can be written in the form \( y' = f(x)g(y), \) where \(f\) and \(g\) are integrable functions in the domain of interest. Treating formally \( y'(x)=dy/dx\) as a fraction, multiplying by \( dx\) and dividing by \( g(y)\), we obtain \( \frac{dy}{g(y)}=f(x)\, dx\). Integrating the left hand side with respect to \( y\) and the right hand side with respect to \( x\), we get
\(\displaystyle \int \frac{\mathrm{d}y}{g(y)} = \int f(x)\, \mathrm{d}x + C\)
This method gives the solution to the differential equation in implicit form, which we may further be able to solve explicitly for \(y =y(x)\). The justification for this formal treatment can be made by using change of variables in integrals.
Example 4.
Let us solve the differential equation \(\displaystyle y'+\frac{2}{5}x = 0 \) by separating the variables. (We could also solve the equation by using the method of integrating factors.)
\(\displaystyle y'+\frac{2}{5}y = 0 \)
\(\displaystyle \frac{dy}{dx} = -\frac{2}{5}y \)
\(\displaystyle \int \frac{1}{y}\, \mathrm{d}y = -\frac{2}{5} \int \, \mathrm{d}x \)
\(\displaystyle \ln |y| = -\frac{2}{5}x + C_1 \)
\( \displaystyle y =\pm e^{-\frac{2}{5}x+C_1} = \pm e^{-\frac{2}{5}x}e^{C_1} = Ce^{-\frac{2}{5}x}, \: C\neq 0. \)
In the last step, we wrote \(C =\pm e^{C_1}\) for simplicity. The case \( C=0\) is also allowed, since it leads to the trivial solution \(y(x)\equiv 0\), see below.
Example 5.
Let us solve the initial value problem
\( \left\{\begin{align}y' = \frac{x}{y} \\ y(0) = 1 \end{align} \right. \)
Because the general solution is not required, we may take a little shortcut by applying integrals in the following way:
\(\displaystyle \frac{dy}{dx} = \frac{x}{y} \)
\(\displaystyle \int_1^y y \, \mathrm{d}y =\int_0^x x \, \mathrm{d}x \)
\(\displaystyle \frac{1}{2}y^2 - \frac{1}{2} =\frac{1}{2}x^2 \)
The solution is \( y=y(x)=\sqrt{x^2+1}\).
The trivial solutions of a separable ODE
General solution achieved by applying the method for separable functions typically lacks information about solutions related to the zeros of the function \(g(y)\). The reason for this is that in the separation method we need to assume that \(g(y(x)) \neq 0\) in order to be able to divide the expression by \(g(y(x))\). We notice that for each zero \(\alpha\) of the function \(g\) there exists a corresponding constant solution \(y(x)\equiv \alpha\) of the ODE \(y'=f(x)g(y)\), since \(y'(x)\equiv 0=g(\alpha)\equiv g(y(x))\). These solutions are called trivial solutions (in contrast to the general solution).
If the conditions of the following theorem hold, then all the solutions to a separable differential equation can be derived from either the general solution or the trivial solutions.
Theorem 2.
Let us consider the initial value problem \(y'=f(x,y),\ y(x_0)=y_0\).
- If \(f\) is continuous (as a function of two variables), then there exists at least one solution in some interval containing the point \(x_0\).
- Also, if \(f\) is continuously differentiable with respect to \(y\), then the solution satisfying the initial condition is unique.
- The uniqueness also holds, when in addition to (i) the function \(f\) is continuously differentiable with respect to \(x\) and \(f(x_0,y_0)\neq 0\).
The proof of the theorem is based on a technique known as Picard-Lindelöf iteration, which was invented by Emile Picard and further developed by the Finnish mathematician Ernst Lindelöf (1870-1946), and others.
Applying the previous theorem, we can formulate the following result for separable equations.
Theorem 3.
Let us consider a separable differential equation \(y'=f(x)g(y)\), where \(f\) is continuous and \(g\) is continuously differentiable.
- For each zero \(\alpha\) of the function \(g\) there exists a trivial solution \(y(x)\equiv \alpha =\) constant.
- All other solutions (= the general solution) can be obtained by applying the previously described method, i.e. separating the variables and calculating the integrals.
The solution curves at each point \((x_0,y_0)\) of the domain of the equation are always unique. In particular, the curves cannot intersect and it is not possible for a single curve to split into two or several parts.
∴ The other solution curves of the ODE cannot intersect the curves \(y=\alpha\) corresponding to the trivial solutions. That is, for all the other solutions the condition \(g(y(x))\neq 0\) automatically holds!
Example 6.
Let us solve the linear homogeneous differential equation \(y'+p(x)y=0\) by applying the method of separation.
The equation has the trivial solution \(y_0(x)\equiv 0\). Since the other solutions do not get the value 0 anywhere, it holds that
\[\begin{aligned} \frac{dy}{dx} &= y'= -p(x)y \\ &\Leftrightarrow \int\frac{\mathrm{d}y}{y} = -\int p(x)\, \mathrm{d}x +C_1 \\ &\Leftrightarrow \ln|y| = -P(x)+C_1 \\ &\Leftrightarrow |y| =e^{C_1-P(x)} \\ &\Leftrightarrow y=y(x)=\pm e^{C_1} e^{-P(x)} =Ce^{-P(x)}.\end{aligned}\]
Here, the expression \(\pm e^{C_1}\) has been replaced by a simpler constant \(C\in\mathbb{R}\).
\(\star\) Equations expressible as separable
Some differential equations can made separable by using a suitable substitution.
i) ODEs of the form \( y'(x)= f\Big(\frac{y(x)}{x}\Big). \)
Example 7.
Let us solve the differential equation \( y'= \frac{x+y}{x-y}. \) The equation is not separable in this form, but we can make if separable by substituting \( u = \frac{y}{x}, \) resulting to \( y' = u + xu'. \) We get
\( u + xu'= \displaystyle \frac{1+u}{1-u}. \)
Separating the variables and integrating both sides, we get
\( \displaystyle \int \frac{1-u}{1+u^2} \, \mathrm{d}u= \int \frac{1}{x} \, \mathrm{d}x \)
\( \arctan{u}
- \displaystyle \frac{1}{2} \ln(u^2 +1)= \ln{x} + C. \)
Substituting \( u = \frac{y}{x} \) and simplifying yields
\( \displaystyle \arctan{\frac{y}{x}} = \ln{C\sqrt{x^2 + y^2}}. \)
Here, it is not possible to derive an expression for y so we have to make do with just the implicit solution. The solutions can be visualized graphically:
As we can see, the solutions are spirals expanding in the positive direction that are suitably cut for demonstration purposes. This is clear from the solutions' polar coordinate representation which we obtain by using the substitution
\(\theta = \displaystyle \arctan{\frac{y}{x}}, r = \sqrt{x^2 + y^2}. \)
Hence, the solution is
\(\theta = \ln(Cr) \Leftrightarrow r = Ce^{\theta}. \)
ii) ODEs of the form \(\displaystyle y' = f(ax+by+c) \)
Another type of differential equation that can be made separable are equations of the form
\(\displaystyle y' = f(ax+by+c).\)
To rewrite the equation as separable, we use the substitution \(\displaystyle u = ax+by+c. \)
Example 8.
Let us find the solution to the differential equation
\(\displaystyle y' =(x-y)^2 +1. \)
Here, a natural substitution is \(\displaystyle u = x-y \Leftrightarrow y = x-u \Rightarrow y' = 1-u'. \) Substitution yields
\( \displaystyle 1-u' =u^2 +1 \)
\( \displaystyle \int -\frac{1}{u^2} \, \mathrm{d}u = \int \, \mathrm{d}x \)
\( \displaystyle \frac{1}{u} = x +C \)
\( \displaystyle y = x - \frac{1}{x +C}. \)
Another type of differential equation that can be made separable are equations of the form
\(\displaystyle y' = f(ax+by+c).\)
To rewrite the equation as separable, we use the substitution \(\displaystyle u = ax+by+c. \)
Example 8.
Let us find the solution to the differential equation
\(\displaystyle y' =(x-y)^2 +1. \)
Here, a natural substitution is \(\displaystyle u = x-y \Leftrightarrow y = x-u \Rightarrow y' = 1-u'. \) Substitution yields
\( \displaystyle 1-u' =u^2 +1 \)
\( \displaystyle \int -\frac{1}{u^2} \, \mathrm{d}u = \int \, \mathrm{d}x \)
\( \displaystyle \frac{1}{u} = x +C \)
\( \displaystyle y = x - \frac{1}{x +C}. \)
\(\star\) Euler's method
In practice, it is usually not feasible to find analytical solutions to differential equations. In these cases, the only choice for us is to resort to numerical methods. A prominent example of this kind of technique is called Euler's method. The idea behind the method is the observation made earlier with direction fields: even if we do not know the solution itself, we are still able to determine the tangents of the solution curve. In other words, we are seeking solutions for the initial value problem
\( \left\{\begin{align}y' = f(x,y) \\ y(x_0) = y_0. \end{align} \right. \)
In Euler's method, we begin the solving process by choosing the step length \( h\) and using the iteration formula
\( \displaystyle y_{k+1} = y_k + hf(x_k, y_k). \)
The iteration starts from the index \( \displaystyle k=0 \) by substituting the given initial value to the right side of the iteration formula. Since \(f(x_k, y_k) = y'(x_k) \) is the slope of the tangent of the solution at \(x_k \), on each step we move the distance expressed by the step length in the direction of the tangent. Because of this, an error occurs, which grows as the step length is increased.
Example 9.
Use the gadget on the right to examine the solution to the initial value problem
\( \left\{\begin{align}y' = \sin(xy) \\ y(x_{0}) = y_{0} \end{align} \right. \)
obtained by using Euler's method and compare the result to the precise solution.
2nd and higher order ODEs
For higher order differential equations it is often impossible to find analytical solutions. In this section, we introduce some special cases for which analytical solutions can be found. Most of these cases are linear differential equations. Our focus is on second order differential equations, as they are more common in practical applications and for them it is more likely for an analytical solution to be found, compared to third or higher order differential equations.
Solving a homogeneous ODE
For second order linear equations, there is no easy way to find a general solution. We begin by examining a homogeneous equation
\( y’’ + p(x)y’ + q(x)y = 0,\)
where \(p\) and \(q\) are continuous functions on their domains. Then, it holds that
1) the equation has linearly independent solutions \(y_1\) and \(y_2\), called fundamental solutions. Roughly speaking, linear independence means that the ratio \(y_2(x)/y_1(x)\) is not constant, so that the solutions are essentially different from each other.
2) the general solution can expressed by means of any linearly independent pair of solutions in the form \(y(x) = C_1y_1(x) + C_2y_2(x) \), where \( C_1\) and \( C_2\) are constants.
3) if the initial values \(y(x_0) = a, y'(x_0) = b\) are fixed, then the solution is unique.
A general method for finding explicitly the fundamental solutions \(y_1(x)\) and \(y_2(x)\) does not exist. To find the solution, a typical approach is to try to make an educated guess about the solution's form and check the details by substituting this into the equation.
The above results can be generalized to higher order homogeneous equations as well, but then the number of required fundamental solutions and initial conditions increases with respect to the order of the equation.
Example 1.
The equation \( y’’-y= 0\) has solutions \( y = e^x\) and \( y = e^{-x}.\) These solutions are linearly independent, so the general solution is of the form \( y(x) = C_1e^x + C_2e^{-x}.\)
Equations with constant coefficients
As a relatively simple special case, let us consider the 2nd order equation
\( y’’ + py’ + qy = 0.\)
In order to solve the equation, we use the guess \( y(x) = e^{\lambda x}\), where \( \lambda\) is an unknown constant. Substituting the guess into the equation yields
\( \lambda^2 e^{\lambda x} + p\lambda e^{\lambda x} + qe^{\lambda x} = 0.\)
\( \lambda^2 + p\lambda + q = 0.\)
The last equation is called the characteristic equation of the ODE. Solving the characteristic equation allows us to find the solutions for the actual ODE. The roots of the characteristic equation can be divided into three cases:
1) The characteristic equation has two distinct real roots. Then, the ODE has the solutions \(y_1(x) = e^{\lambda_1x} \) and \(y_2(x) = e^{\lambda_2x}. \)
2) The characteristic equation has a double root. Then, the ODE has the solutions \(y_1(x) = e^{\lambda x} \) and \(y_2(x) = xe^{\lambda x}. \)
3) The roots of the characteristic equation are of the form \(\lambda = a \pm bi.\) Then, the ODE has the solutions \(y_1(x) = e^{ax}\cos(bx) \) and \(y_2(x) = e^{ax}\sin(bx). \)
The second case can be justified by substitution into the original ODE, and the third case by using the Euler formula \( e^{ix}=\cos x+i\sin x\). With minor changes, these results can also be generalized to higher order differential equations.
Since the characteristic equation has exactly the same coefficients as the original ODE, it is not necessary to derive it again in concrete examples: just write it down by looking at the ODE!
Example 2.
Let us solve the initial value problem
\( \left\{\begin{align}y'' -y' +2y=0 \\ y(0) = 1, y(1)=0 \end{align} \right. \)
The characteristic equation is \(\lambda^2 -\lambda -2 = 0,\) which has the roots \( \lambda_1 = 2\) and \( \lambda_2 = -1.\) Thus, the general solution is \( y(x) = C_1e^{2x} + C_2e^{-x}.\) The constants can be determined by using the initial conditions:
\( \left\{\begin{align}C_1 + C_2=1 \\ e^2C_1 + e^{-1}C_2 = 0 \end{align} \right. \)
\( \left\{\begin{align}C_1 = -\frac{1}{e^3-1} \\ C_2 = \frac{e^3}{e^3-1} \end{align} \right. \)
Hence, the general solution is \( y(x) = \frac{1}{e^3-1} (-e^{2x} + e^{3-x}).\)
Example 3.
Let us have a look at how the above results hold in higher order equations by solving
\( y^{(4)} - 4y''' +14y'' -20y' +25y = 0.\)
Now, the characteristic equation is \( \lambda^4 - 4\lambda^3 +14\lambda^2 -20\lambda +25 = 0,\) which has the roots \( \lambda_1 = \lambda_2 = 1 + 2i\) and \( \lambda_3 = \lambda_4 = 1 - 2i.\) Thus, the fundamental solutions to the ODE are \(e^x\sin(2x)\), \(e^x\cos(2x)\), \(xe^x\sin(2x)\) and \(xe^x\cos(2x)\). The general solution is
\( y = C_1e^x\sin(2x) + C_2e^x\cos(2x) + C_3xe^x\sin(2x) + C_4xe^x\cos(2x).\)
For second order linear equations, there is no easy way to find a general solution. We begin by examining a homogeneous equation
\( y’’ + p(x)y’ + q(x)y = 0,\)
where \(p\) and \(q\) are continuous functions on their domains. Then, it holds that
1) the equation has linearly independent solutions \(y_1\) and \(y_2\), called fundamental solutions. Roughly speaking, linear independence means that the ratio \(y_2(x)/y_1(x)\) is not constant, so that the solutions are essentially different from each other.
2) the general solution can expressed by means of any linearly independent pair of solutions in the form \(y(x) = C_1y_1(x) + C_2y_2(x) \), where \( C_1\) and \( C_2\) are constants.
3) if the initial values \(y(x_0) = a, y'(x_0) = b\) are fixed, then the solution is unique.
A general method for finding explicitly the fundamental solutions \(y_1(x)\) and \(y_2(x)\) does not exist. To find the solution, a typical approach is to try to make an educated guess about the solution's form and check the details by substituting this into the equation.
The above results can be generalized to higher order homogeneous equations as well, but then the number of required fundamental solutions and initial conditions increases with respect to the order of the equation.
Example 1.
The equation \( y’’-y= 0\) has solutions \( y = e^x\) and \( y = e^{-x}.\) These solutions are linearly independent, so the general solution is of the form \( y(x) = C_1e^x + C_2e^{-x}.\)
Equations with constant coefficients
As a relatively simple special case, let us consider the 2nd order equation
\( y’’ + py’ + qy = 0.\)
In order to solve the equation, we use the guess \( y(x) = e^{\lambda x}\), where \( \lambda\) is an unknown constant. Substituting the guess into the equation yields
\( \lambda^2 e^{\lambda x} + p\lambda e^{\lambda x} + qe^{\lambda x} = 0.\)
\( \lambda^2 + p\lambda + q = 0.\)
The last equation is called the characteristic equation of the ODE. Solving the characteristic equation allows us to find the solutions for the actual ODE. The roots of the characteristic equation can be divided into three cases:
1) The characteristic equation has two distinct real roots. Then, the ODE has the solutions \(y_1(x) = e^{\lambda_1x} \) and \(y_2(x) = e^{\lambda_2x}. \)
2) The characteristic equation has a double root. Then, the ODE has the solutions \(y_1(x) = e^{\lambda x} \) and \(y_2(x) = xe^{\lambda x}. \)
3) The roots of the characteristic equation are of the form \(\lambda = a \pm bi.\) Then, the ODE has the solutions \(y_1(x) = e^{ax}\cos(bx) \) and \(y_2(x) = e^{ax}\sin(bx). \)
The second case can be justified by substitution into the original ODE, and the third case by using the Euler formula \( e^{ix}=\cos x+i\sin x\). With minor changes, these results can also be generalized to higher order differential equations.
Since the characteristic equation has exactly the same coefficients as the original ODE, it is not necessary to derive it again in concrete examples: just write it down by looking at the ODE!
Example 2.
Let us solve the initial value problem
\( \left\{\begin{align}y'' -y' +2y=0 \\ y(0) = 1, y(1)=0 \end{align} \right. \)
The characteristic equation is \(\lambda^2 -\lambda -2 = 0,\) which has the roots \( \lambda_1 = 2\) and \( \lambda_2 = -1.\) Thus, the general solution is \( y(x) = C_1e^{2x} + C_2e^{-x}.\) The constants can be determined by using the initial conditions:
\( \left\{\begin{align}C_1 + C_2=1 \\ e^2C_1 + e^{-1}C_2 = 0 \end{align} \right. \)
\( \left\{\begin{align}C_1 = -\frac{1}{e^3-1} \\ C_2 = \frac{e^3}{e^3-1} \end{align} \right. \)
Hence, the general solution is \( y(x) = \frac{1}{e^3-1} (-e^{2x} + e^{3-x}).\)
Example 3.
Let us have a look at how the above results hold in higher order equations by solving
\( y^{(4)} - 4y''' +14y'' -20y' +25y = 0.\)
Now, the characteristic equation is \( \lambda^4 - 4\lambda^3 +14\lambda^2 -20\lambda +25 = 0,\) which has the roots \( \lambda_1 = \lambda_2 = 1 + 2i\) and \( \lambda_3 = \lambda_4 = 1 - 2i.\) Thus, the fundamental solutions to the ODE are \(e^x\sin(2x)\), \(e^x\cos(2x)\), \(xe^x\sin(2x)\) and \(xe^x\cos(2x)\). The general solution is
\( y = C_1e^x\sin(2x) + C_2e^x\cos(2x) + C_3xe^x\sin(2x) + C_4xe^x\cos(2x).\)
Example 4.
Let \( \omega >0\) be a constant. The characteristic equation of the ODE \[ y''+\omega^2y=0 \] is \( \lambda^2+\omega^2=0\) with roots \( \lambda=\pm i \omega\). So \( \alpha =0\) and \( \beta =\omega\) in Case 3). Since this ODE is a model for harmonic oscillation, we use time \( t\) as variable, and obtain the general solution \[ y(t)=A\cos (\omega t) +B\sin (\omega t), \] with \( A,B \) constants. They will be uniquely determined if we know the initial location \(y(0)\) and the initial velocity \(y'(0)\). All solutions are periodic and their period is \(T=2\pi/\omega\). In the animation to the right we have \( y'(0)=0\) and you can choose \( \omega\) and the initial displacement \( y(0)=y_0\).
where \(t\) is the elapsed time in seconds
Euler's differential equation
Another relatively common type of 2nd order differential equation is Euler's differential equation
\( x^2y'' + axy' + by = 0,\)
where \(a\) and \(b\) are constants. An equation of this form is solved by using the guess \(y(x)= x^r\). Substituting the guess in the equation yields
\( r^2 + (a-1)r + b = 0.\)
Using the roots of this equation, we obtain the solutions for the ODE in the following way:
1) If the roots are distinct and real, then \( y_1(x)= |x|^{r_1}\) and \( y_2(x)= |x|^{r_2}\).
2) If the equation has a double root, then \( y_1(x)= |x|^{r}\) and \( y_2(x)= |x|^{r}\ln |x|\).
3) If the equation has roots of the form \(r = a \pm bi\), then \( y_1(x)= |x|^{a}\cos(b\ln |x|)\) and \( y_2(x)= |x|^{a}\sin(b\ln |x|)\).
Example 5.
Let us solve the equation \( x^2y'' - 3xy' + y = 0.\) Noticing that the equation is Euler's differential equation, we proceed by using the guess \(y= x^r.\) Substituting the guess into the equation, we get \( r(r-1)x^r - 3rx^r + x^r = 0 \Rightarrow r^2 - 4r + 1 = 0,\) which yields \( r = 2 \pm \sqrt{3}.\) Therefore, the general solution to the ODE is
\(y = C_1 x^{2+\sqrt{3}} + C_2x^{2-\sqrt{3}}\).
Another relatively common type of 2nd order differential equation is Euler's differential equation
\( x^2y'' + axy' + by = 0,\)
where \(a\) and \(b\) are constants. An equation of this form is solved by using the guess \(y(x)= x^r\). Substituting the guess in the equation yields
\( r^2 + (a-1)r + b = 0.\)
Using the roots of this equation, we obtain the solutions for the ODE in the following way:
1) If the roots are distinct and real, then \( y_1(x)= |x|^{r_1}\) and \( y_2(x)= |x|^{r_2}\).
2) If the equation has a double root, then \( y_1(x)= |x|^{r}\) and \( y_2(x)= |x|^{r}\ln |x|\).
3) If the equation has roots of the form \(r = a \pm bi\), then \( y_1(x)= |x|^{a}\cos(b\ln |x|)\) and \( y_2(x)= |x|^{a}\sin(b\ln |x|)\).
Example 5.
Let us solve the equation \( x^2y'' - 3xy' + y = 0.\) Noticing that the equation is Euler's differential equation, we proceed by using the guess \(y= x^r.\) Substituting the guess into the equation, we get \( r(r-1)x^r - 3rx^r + x^r = 0 \Rightarrow r^2 - 4r + 1 = 0,\) which yields \( r = 2 \pm \sqrt{3}.\) Therefore, the general solution to the ODE is
\(y = C_1 x^{2+\sqrt{3}} + C_2x^{2-\sqrt{3}}\).
Nonhomogeneous linear differential equations
The general solution to a nonhomogeneous equation
\(y'' + p(x)y' + q(x)y = r(x)\)
is the general solution to the corresponding homogeneous equation \(+\) particular solution to the nonhomogeneous equation, i.e.
\(y(x) = C_1y_1(x) + C_2y_2(x) + y_0(x)\).
The particular solution \(y_0\) is usually found by using a guess that is of the same form as \(r(x)\) with general coefficients. Substituting the guess into the ODE, we can solve these coefficients, but only if the guess is of the correct form.
In the table below, we have created a list of possible guesses for second order differential equations with constant coefficients. The form of the guess depends on what kind of elementary functions \(r(x)\) consists of. If \(r(x)\) is a combination of several different elementary functions, then we need to include corresponding elements for all of these functions in our guess. The characteristic equation of the corresponding homogeneous differential equation is \(P(\lambda)=\lambda^2+p\lambda+q=0\).
\(r(x)\) contains
the guess consists of
\(n\)th degree polynomial
\(A_0+A_1x+\dots +A_nx^n\) ( \(+A_{n+1}x^{n+1}\), if \(q=P(0)=0\))
\(\sin kx,\ \cos kx\)
\(A\cos kx+B\sin kx\), if \(P(ik)\neq 0\)
\(\sin kx,\ \cos kx\)
\(Ax\cos kx+Bx\sin kx\), if \(P(ik)=0\)
\(e^{cx}\sin kx,\ e^{cx}\cos kx\)
\(Ae^{cx}\cos kx+Be^{cx}\sin kx\), if
\(P(c+ik)\neq 0\)
\(e^{kx}\)
\(Ae^{kx}\), if \(P(k)\neq 0\)
\(e^{kx}\)
\(Axe^{kx}\), if \(P(k)=0\) and \(P'(k)\neq 0\)
\(e^{kx}\)
\(Ax^2e^{kx}\), if \(P(k)=P'(k)=0\)
Note. For roots of a second degree polynomial we have to keep in mind that
\(P(k)=0\) and \(P'(k)\neq 0\) \(\Leftrightarrow\) \(k\in\mathbb{R}\) is a simple root of \(P\).
\(P(k)=P'(k)= 0\) \(\Leftrightarrow\) \(k\in\mathbb{R}\) is a double root of \(P\).
\(P(ik)\neq 0\) \(\Leftrightarrow\) \(ik\in\mathbb{C}\) is not a root of \(P\); i.e. \(\sin kx\) and \(\cos kx\) are not solutions to the homogeneous equation.
Example 6.
Let us find the general solution to the ODE \(y''+y'-6y=r(x)\), when
a) \(r(x)=12e^{-x}\)
b) \(r(x)=20e^{2x}\).
The solutions are of the form \(y(x)=C_1e^{-3x}+C_2e^{2x}+y_0(x)\).
a) Substituting the guess \(y_0(x)=Ae^{-x},\) we get
\((A -A -6A)e^{-x} =12e^{-x}\),
which solves for \(A=-2\).
b) In this case a guess of the form \(Be^{2x}\) is useless, as it is part of the general solution to the corresponding homogeneous equation and yields just zero when substituted to the left side of the ODE. Here, a right guess is of the form \(y_0(x)=Bxe^{2x}\). Substitution yields
\[
(4B+2B-6B)xe^{2x}+(4B+B)e^{2x} = 20e^{2x},
\]
which solves for \(B=4\).
Using these values for \(A\) and \(B\), we can write the general solutions to the given differential equations.
Example 7.
Let us find the solution to the ODE \(y''+y'-6y=12e^{-x}\) with the initial conditions
\(y(0)=0\), \(y'(0)=6\).
Based on the previous example, the general solution is of the form
\(y(x)=C_1e^{-3x}+C_2e^{2x}-2e^{-x}\). Differentiation yields
\(y'(x)=-3C_1e^{-3x}+2C_2e^{2x}+2e^{-x}\). From the initial conditions, we get the following pair of equations:
\[
\begin{cases}
0=y(0)=C_1+C_2-2 &\\
6=y'(0)=-3C_1+2C_2+2, &\\
\end{cases}
\]
which solves for \(C_1=0\) and \(C_2=2\). Therefore, the solution to the initial value problem is
\(y(x)=2e^{2x}-2e^{-x}\).
Example 8.
A typical application of a second order nonhomogeneous ODE is an RLC circuit containing a resistor (with resistance \( R\)), an inductor (with inductance \( L \)), a capacitor (with capacitance \( C \)), and a time-dependent electromotive force \( E(t)\). The electric current \( y(t)\) in the circuit satisfies the ODE \[ Ly''+Ry'+\frac{1}{C}y=E'(t).\] Let us solve this ODE with artificially chosen numerical values in the form \[ y''+10y'+61y=370\sin t.\]
The homogeneous part has characteristic equation of the form
\( \lambda^2+10\lambda +61=0\) with solutions \( \lambda = -5\pm 6i\). This gives the solutions \( y_1(t)=e^{-5t}\cos(6t)\) and \( y_2(t)=e^{-5t}\sin(6t) \) for the homogeneous equation. For a particular solution we try \(y_0(t)=A\cos t +B\sin t\). Substituting this into the nonhomogeneous ODE and collecting similar terms yields to \[ (60A+10B)\cos t +(60B-10A)\sin t = 370\sin t. \] This equation will be
satisfied for all \( t\) (only) if
\[
\begin{cases}
60A+10B=0 &\\
-10A+60B=370. &\\
\end{cases}
\]
which solves for \( A=-1\) and \( B=6\). Therefore, the general solution is
\[ y(t)=e^{-5t}(C_1\cos(6t)+C_2\sin(6t)) -\cos t+6\sin t .\]
Note. The exponential terms go to zero very fast and eventually, the current oscillates in the form \[ y(t)\approx -\cos t+6\sin t.\]
The general solution to a nonhomogeneous equation
\(y'' + p(x)y' + q(x)y = r(x)\)
is the general solution to the corresponding homogeneous equation \(+\) particular solution to the nonhomogeneous equation, i.e.
\(y(x) = C_1y_1(x) + C_2y_2(x) + y_0(x)\).
The particular solution \(y_0\) is usually found by using a guess that is of the same form as \(r(x)\) with general coefficients. Substituting the guess into the ODE, we can solve these coefficients, but only if the guess is of the correct form.
In the table below, we have created a list of possible guesses for second order differential equations with constant coefficients. The form of the guess depends on what kind of elementary functions \(r(x)\) consists of. If \(r(x)\) is a combination of several different elementary functions, then we need to include corresponding elements for all of these functions in our guess. The characteristic equation of the corresponding homogeneous differential equation is \(P(\lambda)=\lambda^2+p\lambda+q=0\).
| \(r(x)\) contains |
the guess consists of |
|---|---|
| \(n\)th degree polynomial |
\(A_0+A_1x+\dots +A_nx^n\) ( \(+A_{n+1}x^{n+1}\), if \(q=P(0)=0\)) |
| \(\sin kx,\ \cos kx\) |
\(A\cos kx+B\sin kx\), if \(P(ik)\neq 0\) |
| \(\sin kx,\ \cos kx\) | \(Ax\cos kx+Bx\sin kx\), if \(P(ik)=0\) |
| \(e^{cx}\sin kx,\ e^{cx}\cos kx\) | \(Ae^{cx}\cos kx+Be^{cx}\sin kx\), if \(P(c+ik)\neq 0\) |
| \(e^{kx}\) | \(Ae^{kx}\), if \(P(k)\neq 0\) |
| \(e^{kx}\) | \(Axe^{kx}\), if \(P(k)=0\) and \(P'(k)\neq 0\) |
| \(e^{kx}\) | \(Ax^2e^{kx}\), if \(P(k)=P'(k)=0\) |
Note. For roots of a second degree polynomial we have to keep in mind that
\(P(k)=0\) and \(P'(k)\neq 0\) \(\Leftrightarrow\) \(k\in\mathbb{R}\) is a simple root of \(P\).
\(P(k)=P'(k)= 0\) \(\Leftrightarrow\) \(k\in\mathbb{R}\) is a double root of \(P\).
\(P(ik)\neq 0\) \(\Leftrightarrow\) \(ik\in\mathbb{C}\) is not a root of \(P\); i.e. \(\sin kx\) and \(\cos kx\) are not solutions to the homogeneous equation.
Example 6.
Let us find the general solution to the ODE \(y''+y'-6y=r(x)\), when
a) \(r(x)=12e^{-x}\)
b) \(r(x)=20e^{2x}\).
The solutions are of the form \(y(x)=C_1e^{-3x}+C_2e^{2x}+y_0(x)\).
a) Substituting the guess \(y_0(x)=Ae^{-x},\) we get \((A -A -6A)e^{-x} =12e^{-x}\), which solves for \(A=-2\).
b) In this case a guess of the form \(Be^{2x}\) is useless, as it is part of the general solution to the corresponding homogeneous equation and yields just zero when substituted to the left side of the ODE. Here, a right guess is of the form \(y_0(x)=Bxe^{2x}\). Substitution yields
\[ (4B+2B-6B)xe^{2x}+(4B+B)e^{2x} = 20e^{2x}, \]which solves for \(B=4\).
Using these values for \(A\) and \(B\), we can write the general solutions to the given differential equations.
Example 7.
Let us find the solution to the ODE \(y''+y'-6y=12e^{-x}\) with the initial conditions \(y(0)=0\), \(y'(0)=6\).
Based on the previous example, the general solution is of the form \(y(x)=C_1e^{-3x}+C_2e^{2x}-2e^{-x}\). Differentiation yields \(y'(x)=-3C_1e^{-3x}+2C_2e^{2x}+2e^{-x}\). From the initial conditions, we get the following pair of equations:
\[ \begin{cases} 0=y(0)=C_1+C_2-2 &\\ 6=y'(0)=-3C_1+2C_2+2, &\\ \end{cases} \]which solves for \(C_1=0\) and \(C_2=2\). Therefore, the solution to the initial value problem is \(y(x)=2e^{2x}-2e^{-x}\).
Example 8.
A typical application of a second order nonhomogeneous ODE is an RLC circuit containing a resistor (with resistance \( R\)), an inductor (with inductance \( L \)), a capacitor (with capacitance \( C \)), and a time-dependent electromotive force \( E(t)\). The electric current \( y(t)\) in the circuit satisfies the ODE \[ Ly''+Ry'+\frac{1}{C}y=E'(t).\] Let us solve this ODE with artificially chosen numerical values in the form \[ y''+10y'+61y=370\sin t.\]
The homogeneous part has characteristic equation of the form \( \lambda^2+10\lambda +61=0\) with solutions \( \lambda = -5\pm 6i\). This gives the solutions \( y_1(t)=e^{-5t}\cos(6t)\) and \( y_2(t)=e^{-5t}\sin(6t) \) for the homogeneous equation. For a particular solution we try \(y_0(t)=A\cos t +B\sin t\). Substituting this into the nonhomogeneous ODE and collecting similar terms yields to \[ (60A+10B)\cos t +(60B-10A)\sin t = 370\sin t. \] This equation will be satisfied for all \( t\) (only) if
\[ \begin{cases} 60A+10B=0 &\\ -10A+60B=370. &\\ \end{cases} \]which solves for \( A=-1\) and \( B=6\). Therefore, the general solution is \[ y(t)=e^{-5t}(C_1\cos(6t)+C_2\sin(6t)) -\cos t+6\sin t .\] Note. The exponential terms go to zero very fast and eventually, the current oscillates in the form \[ y(t)\approx -\cos t+6\sin t.\]