Differentiaali- ja integraalilaskenta 2

Tasointegraali

Olkoon \(D\subset \mathbb{R}^2\) joukko tasossa ja \(f\colon D\to \mathbb{R}\) skalaarikenttä. Halutaan määritellä tasointegraali \[ \iint_D f(x,y)\,dA. \] Integraalin arvo on pinnan \(z=f(x,y)\) ja \(xy\)-tason väliin jäävän alueen tilavuus.

Tutkitaan aluksi erikoistapausta \(D=[a,b]\times [c,d]\).

Yhden muuttujan tapaus

Yhden muuttujan tapauksessa integraali saadaan Riemannin summien raja-arvona.

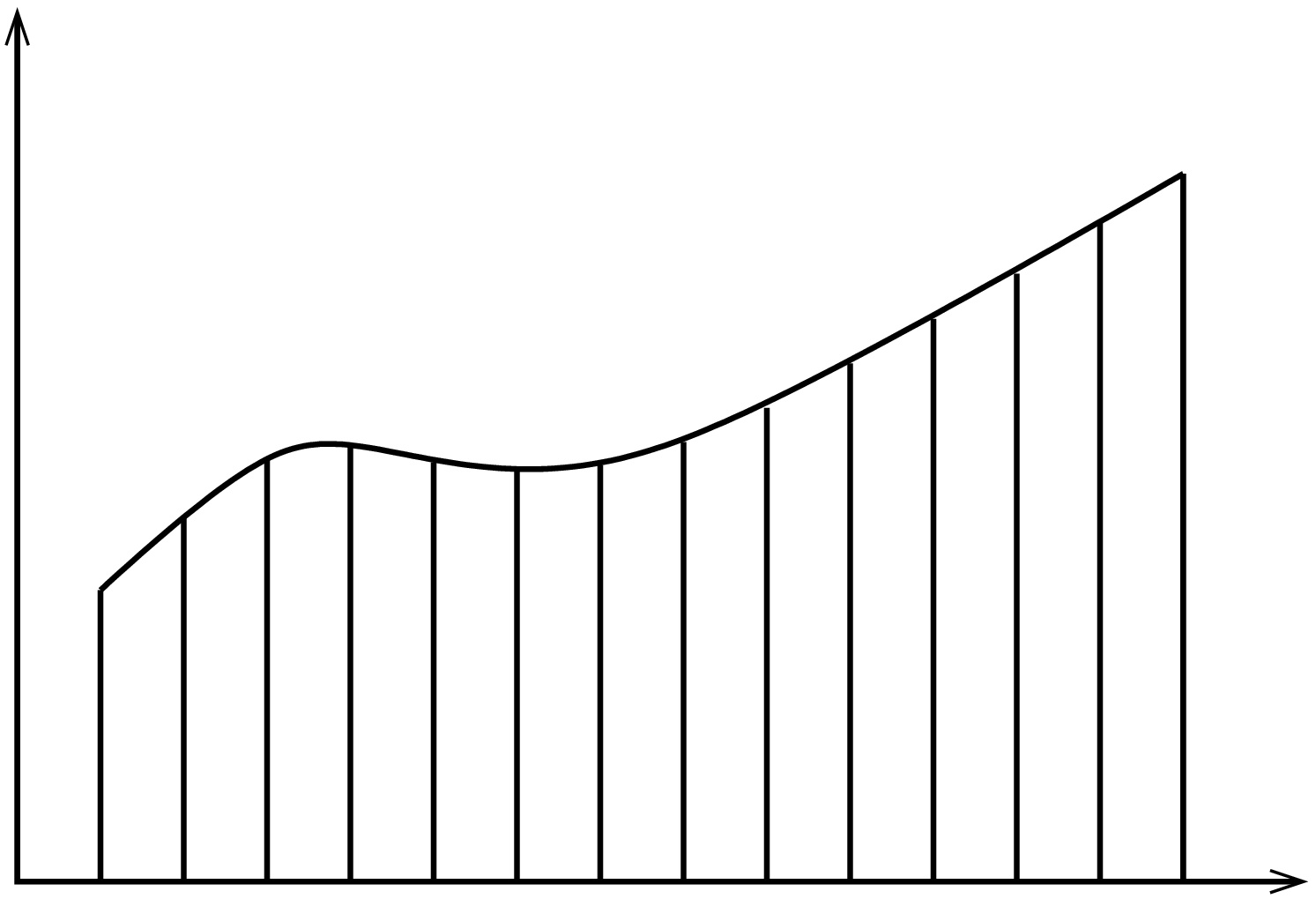
Formaalisti \[ \int_a^b f(x)\,dx = \lim_{n\to\infty} \sum_{i=1}^n f(x_i)\Delta x, \] missä \(a=x_0 < x_1 < \ldots < x_n=b\) on välin \([a,b]\) tasavälinen jako ja \(\Delta x\) on jakovälin pituus.

Usean muuttujan tapaus (tasointegraali, \(\mathbb{R}^2\))

Jaetaan tason osajoukko \(D=[a,b]\times [c,d]\) tasavälisesti ruudukoksi niin, että kummallakin akselilla on \(n\) jakopistettä.

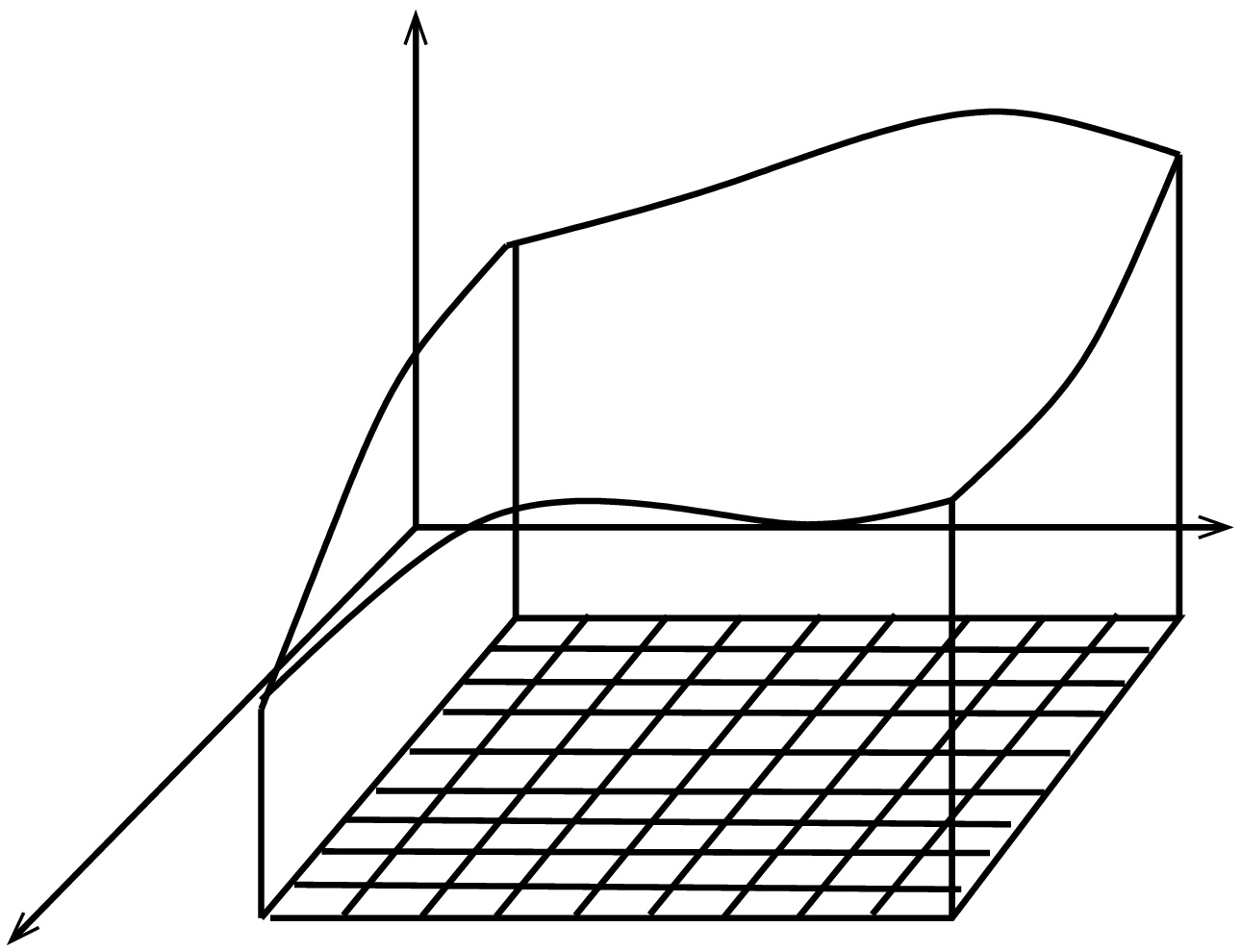
Nyt voidaan määritellä \[ \iint_D f(x,y)\,dA = \lim_{n\to\infty} \sum_{i=1}^n\sum_{j=1}^n f(x_i,y_j)\,\Delta x\Delta y, \] missä \[x_{i} = a + i\frac{b-a}{n},\qquad y_{j} = c + j\frac{d-c}{n}\] ja \(\Delta x\) sekä \(\Delta y\) vastaavat jakovälien pituutta \(x\) ja \(y\)-suunnassa: \[ \Delta x= \frac{b-a}{n},\quad \Delta y = \frac{d-c}{n}. \]

Usean muuttujan tapaus (avaruusintegraali, \(\mathbb{R}^3\))

Tason tapauksessa edellä määriteltyä integraalia kutsutaan tasointegraaliksi. Samaan tapaan voidaan määritellä avaruusintegraali: \[ \iiint_D f(x,y,y)\,dV = \lim_{n\to\infty} \sum_{i=1}^n\sum_{j=1}^n\sum_{k=1}^n f(x_i,y_j,z_k)\,\Delta x\Delta y\Delta z, \] kun \(D=[a_1,b_1]\times [a_2,b_2]\times[a_3,b_3] \subset \mathbb{R}^2\) ja \(f\colon D\to \mathbb{R}\). Tässä \[ \Delta x = \frac{b_1-a_1}{n},\quad \Delta y = \frac{b_2-a_2}{n}\text{ ja } \Delta z = \frac{b_3-a_3}{n}. \] Vieläkin useamman muuttujan funktioita \(f\colon D\subset \mathbb{R}^n\to\mathbb{R}\), missä \(n\ge 2\), voi integroida samaan tapaan.

Huomautuksia

Yhden muuttujan tapauksessa integraaleille pätee Analyysin (ensimmäinen) peruslause: \[ f(x)=\frac{d}{dx}\int_c^x f(t)\,dt,\textrm{ kun }c,x\in[a,b] \] ja \(f\colon [a,b]\to\mathbb{R}\) on jatkuva funktio.

Analyysin peruslauseesta seuraa, että integrointi ja derivointi ovat toistensa vastaoperaatiota, mikä johtaa moniin integroinnissa hyödyllisiin kaavoihin. Analyysin peruslauseella ei kuitenkaan ole aivan samanlaista vastinetta usean muuttujan tapauksessa; Greenin, Gaussin ja Stokesin lauseet ovat kuitenkin sille sukua.

Moninkertainen integraali

Monen muuttujan integraaleja voidaan usein kuitenkin laskea moninkertaisina integraaleina. Kaksiulotteinen tapaus (integrointialue suorakulmio) \[ \iint_D f(x,y)\,dA = \int_c^d \int_a^b f(x,y)\,dx\,dy,\text{ kun } D=[a,b]\times [c,d]. \] Kolmiulotteinen tapaus (integrointialue suorakulmainen särmiö) \[ \iiint_D f(x,y,z)\,dV = \int_{a_3}^{b_3}\int_{a_2}^{b_2}\int_{a_1}^{b_1} f(x,y,z)\,dx\,dy\,dz, \] kun \(D=[a_1,b_1]\times [a_2,b_2]\times [a_3,b_3]\).

Mikäli funktio \(f\colon \mathbb{R}^n \to \mathbb{R}\) (\(n=2,3,\ldots\)) on jatkuva, niin integroimisjärjestyksellä ei ole väliä integraalin arvon kannalta. Laskujen helppouden kannalta väliä kuitenkin on.

Esimerkki

Olkoon \(f(x,y)=xy^2\). Lasketaan \[ \iint_D f(x,y)\,dA,\text{ kun } D=\{(x,y)\in \mathbb{R}^2: 0\le x\le1, \,0\le y\le 1\}. \]
Aluksi kirjoitetaan tasointegraali kaksinkertaisena integraalina, ja lasketaan \begin{align*} \iint_D xy^2\,dA &= \int_0^1\int_0^1 xy^2\,dx\,dy = \int_0^1\bigg[\frac{x^2y^2}{2}\bigg]_{x=0}^{1}\,dy \\ &= \int_0^1 \frac{y^2}{2}\,dy \bigg[\frac{y^3}{6}\bigg]_{y=0}^1 = \frac{1}{6}. \end{align*}

Esimerkki

Olkoon \(f(x,y,z)=xye^z\). Lasketaan \[ \iiint_D f(x,y,z)\,dV,\text{ missä } D=[0,2]\times [0,1] \times [-1,1]. \]
Kirjoitetaan avaruusintegraali kolminkertaisena integraalina. Lasketaan \begin{align*} &\iiint_D xye^z\,dV = \int_{-1}^1\int_0^1\int_0^2 xye^z\,dx\,dy\,dz \\ &\quad = \int_{-1}^1\int_0^1 \frac{x^2ye^z}{2}\bigg|_{x=0}^2\,dy\,dz = \int_{-1}^1\int_0^1 2ye^z\,dy\,dz \\ &\quad = \int_{-1}^1 y^2e^z\bigg|_{y=0}^1\,dz = \int_{-1}^1 e^z\,dz = e^z\Big|_{z=-1}^1 = e -e^{-1}. \end{align*}

Integrointi yleisemmissä alueissa

Tutkitaan funktiota \(f\colon D\to \mathbb{R}\), joka on määritelty tason (tai avaruuden) osajoukossa \(D\). Tähän asti on oletettu, että \(D\) on suorakaide (vast. suorakulmainen särmiö). Yleisemmässä tapauksessa voidaan tarkastella suorakulmiota \(\hat D\), jolle \(D\subset \hat D\). Jotta integraali olisi määritelty, täytyy joukon \(D\) olla ''siisti'' (riittää esimerkiksi, että reuna on paloittain sileä).

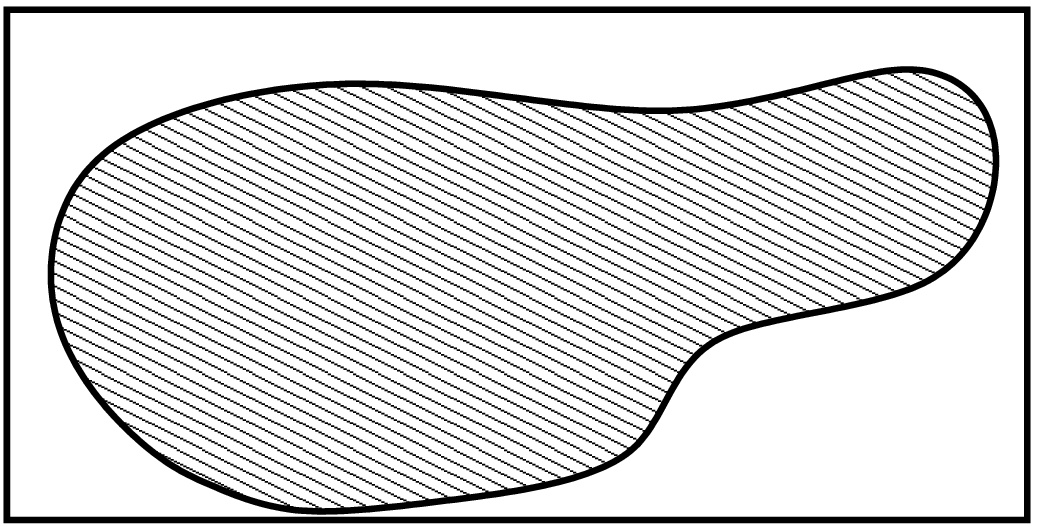
Määritellään funktio \(\hat f\colon \hat D \to \mathbb{R}\) seuraavasti: \[ \hat f(x,y) = \left\{ \begin{array}{rcl} f(x,y), &\text{kun} &(x,y) \in D,\\ 0, & \text{kun} & (x,y) \in \hat D \setminus D. \end{array}\right. \] Nyt voidaan määritellä \[ \iint_D f(x,y)\,dA := \iint_{\hat D} \hat f(x,y)\,dA. \] Samaan tapaan voidaan määritellä myös avaruusintegraali ei-suorakulmaisen integroimisalueen tapauksessa: \[ \iiint_D f(x,y,z)\,dV := \iiint_{\hat D} \hat f(x,y,z)\,dV, \] kun \(\hat D\) on suorakulmainen särmiö ja \(D \subset \hat D\).

Esimerkki

Olkoon \( D=\{(x,y)\in \mathbb{R}^2 : 0 < x < 1,\, 0 < y < x\} \). Lasketaan funktion \(f(x,y)=xy\) integraali yli alueen \(D\).

\begin{align*} &\iint_D xy\,dA = \int_0^1\bigg(\int_0^x xy\,dy\bigg)dx \\ &\quad \int_0^1\frac{xy^2}{2}\bigg|_{y=0}^x\,dx = \int_0^1\frac{x^3}{2}\,dx = \frac{x^4}{8}\bigg|_{x=0}^1 =\frac{1}{8}. \end{align*} Integrointi on mahdollista suorittaa myös toisessa järjestyksessä: \begin{align*} &\iint_D xy\,dA = \int_0^1\bigg(\int_y^1 xy\,dx\bigg)dy \\ &\quad = \int_0^1\frac{x^2y}{2}\bigg|_{x=y}^1\,dy = \int_0^1\frac{y}{2}-\frac{y^3}{2}\,dy \\ &\quad = \bigg[\frac{y^2}{4}-\frac{y^4}{8}\bigg]_{y=0}^1 = \frac{1}{4}-\frac{1}{8} = \frac{1}{8}. \\ \end{align*}

Esimerkki

Lasketaan funktion \(f(x,y)=e^{x^2}\) integraali edellisen esimerkin alueessa.

\[ \iint_D e^{x^2}\,dA = \int_0^1\bigg(\int_0^x e^{x^2}\,dy\bigg)dx =\int_0^1 xe^{x^2}\,dx \] Sijoituksella \(t=x^2\), \(dt=2x\,dx\) saadaan \[ \frac{1}{2}\int_0^1e^t\,dt = \frac{1}{2}e^t\bigg|_{t=0}^1 = \frac{e}{2}-\frac{1}{2}. \]